Posebna točka. Izolirane singularne točke Primer izolirane singularne točke

Taylorjeve serije služijo kot učinkovito orodje za preučevanje funkcij, ki so analitične v krogu zol Za preučevanje funkcij, ki so analitične v obročastem območju, se izkaže, da je mogoče konstruirati razširitve v pozitivnih in negativnih potencah (z - zq) obliki, ki posplošuje Taylorjeve razširitve. Niz (1), ki ga razumemo kot vsoto dveh nizov, imenujemo Laurentov niz. Jasno je, da je območje konvergence serije (1) skupni del območij konvergence vsakega od nizov (2). Poiščimo jo. Območje konvergence prve serije je krog, katerega polmer je določen s formulo Cauchy-Hadamard Znotraj konvergenčnega kroga serija (3) konvergira k analitični funkciji in v vsakem krogu manjšega polmera konvergira absolutno in enotno. Druga vrsta je potenčna vrsta glede na spremenljivko. Vrsta (5) konvergira v svojem konvergenčnem krogu k analitični funkciji kompleksne spremenljivke m-*oo, v kateremkoli krogu manjšega polmera pa konvergira absolutno in enakomerno, kar pomeni, da je konvergenčno območje niza (4) videz kroga - Če potem obstaja skupno konvergenčno območje niza (3) in (4) - krožni obroč, v katerem konvergira niz (1) na analitično funkcijo. Poleg tega se v katerem koli obroču konvergira absolutno in enakomerno. Primer 1. Določite območje konvergence rad Laurentove vrste. Izolirane singularne točke in njihovo klasifikacijo (z), ki je enovrednotna in apolitična v krožnem obroču, lahko v tem obroču predstavimo kot vsoto konvergentne vrste, katere koeficienti Cn so enolično določeni in izračunani po formulah kjer je 7p krog s polmerom m Fiksirajmo poljubno točko z znotraj obroča R Konstruiramo kroge s središči v točki r0, katerih polmeri zadoščajo neenačbam, in obravnavamo nov obroč Po Cauchyjevem integralskem izreku za večpovezano področje imamo Transformirajmo vsakega od integralov v vsoti (8) posebej. Za vse točke £ vzdolž kroga 7d* je izpolnjena relacija de vsota enakomerno konvergentnega niza 1 1. Zato lahko ulomek ^ predstavimo v vi- /" / Za vse točke £ na krogu ir> zveza je izpolnjeno. Zato lahko ulomek ^ predstavimo kot vsoto enakomerno konvergentnega niza v formulah (10) in (12) sta analitični funkciji v krožnem obroču. Zato se po Cauchyjevem izreku vrednosti ustreznih integralov ne spremenijo, če kroga 7/r in 7r/ zamenjamo s poljubnim krogom. To nam omogoča, da združimo formuli (10) in (12). Če zamenjamo integrale na desni strani formule (8) z njihovimi izrazi (9) oziroma (11), dobimo želeno razširitev. Ker je z poljuben točki obroča sledi, da niz ( 14) konvergira k funkciji f(z) povsod v tem obroču in v katerem koli obroču konvergira niz k tej funkciji absolutno in enakomerno. Dokažimo zdaj, da je razpad oblike (6) edinstven. Predpostavimo, da se zgodi še ena dekompozicija, potem imamo povsod znotraj obroča R Na obodu niz (15) enakomerno konvergira. Pomnožite obe strani enakosti (kjer je m fiksno celo število in integrirajte obe vrsti člen za členom. Posledično dobimo na levi strani in na desni strani - Csh. Tako je (4, \u003d St. Ker je m poljubno število, se zadnji niz enakosti (6), katerega koeficiente izračunamo po formulah (7), imenuje Laurentov niz funkcije f(z) v obroču 7) za koeficiente Laurentove vrste se v praksi redko uporabljajo, ker praviloma zahtevajo okorne izračune. Običajno, če je mogoče, se uporabljajo že pripravljene Taylorjeve razširitve elementarnih funkcij. Glede na edinstvenost razširitve vsaka legitimna metoda vodi do istega. rezultat. Primer 2. Upoštevajte Laurentove razporeditve funkcij različnih domen ob predpostavki, da ima Fuiscija /(z) dve singularni točki: Zato obstajajo tri obročne domene in s središčem v točki r = 0. v vsakem od njih je funkcija f(r) analitična: a) krog je zunanjost kroga (slika 27). Poiščimo Laurentove ekspanzije funkcije /(z) v vsakem od teh območij. Predstavimo /(z) kot vsoto elementarnih ulomkov a) Krožnica Transformiraj relacijo (16) na naslednji način Z uporabo formule za vsoto členov geometrijske progresije dobimo b) Obroč za funkcijo -z ostaja v tem obroču konvergenten, saj niz (19) za funkcijo j^j za |z| > 1 se razhaja. Zato transformiramo funkcijo /(z) na naslednji način: s ponovno uporabo formule (19) dobimo, da Ta vrsta konvergira za. Če razširitvi (18) in (21) nadomestimo relacijo (20), dobimo c) Zunanjost kroga za funkcijo -z z |z| > 2 divergira in vrsta (21) za funkcijo Predstavimo funkcijo /(z) v naslednji obliki: /<*> Z uporabo formul (18) in (19) dobimo ALI 1 Ta primer kaže, da ima Laurentova ekspanzija za isto funkcijo f(z) na splošno različno obliko za različne obroče. Primer 3. Poiščite razgradnjo 8 Laurentove vrste funkcije Laurentove vrste Izolirane singularne točke in njihova razvrstitev v obročasto območje A Uporabimo predstavitev funkcije f (z) v naslednji obliki: in transformiramo drugi člen z uporabo formulo za vsoto členov geometrijske progresije dobimo Če najdene izraze zamenjamo v formulo (22), imamo Primer 4. Razširimo funkcijo v Laurentovo vrsto v okolici tankega zq = 0. Za katero koli kompleksno , imamo Naj Ta razširitev velja za katero koli točko z Ф 0. V tem primeru je obročasto območje celotna kompleksna ravnina z eno točko z izločeno - 0. To območje lahko definiramo z naslednjim razmerjem: Ta funkcija je analitična v regiji Iz formul (13) za koeficiente Laurentove vrste lahko z enakim sklepanjem kot v prejšnjem odstavku dobimo Kouiwove neenakosti. če je funkcija f(z) omejena na krog, kjer je M konstanta), potem izolirane singularne točke. Točko zo imenujemo izolirana singularna točka funkcije f(z), če obstaja obročasta soseska točke ( to množico včasih imenujemo tudi prebodena okolica točke 2o), kjer je funkcija f(z) enovrednostna in analitična. V sami točki zo funkcija bodisi ni definirana bodisi ni enovrednostna in analitična. Glede na obnašanje funkcije /(z) pri približevanju točki zo ločimo tri vrste singularnih točk. Izolirana singularna točka se imenuje: 1) odstranljiva, če obstaja končna 2) pmusach, če 3) bistveno singularna točka, če funkcija f(z) nima meje za Izrek 16. Izolirana singularna točka z0 funkcije f(z) je odstranljiva singularna točka, če in samo če Laurentova ekspanzija funkcije f(z) v okolici točke zo ne vsebuje glavnega dela, tj. ima obliko Let zo - odstranljiva singularna točka. Potem obstaja končna in je zato funkcija f(z) omejena v prokološki soseščini točke r. Na podlagi Cauchyjevih neenakosti smo postavili. Ker je p mogoče izbrati kot poljubno majhen, so vsi koeficienti pri negativni potence (z - 20) enake nič: Nasprotno pa naj Laurentova razširitev funkcije /(r) v okolico točke zq vsebuje le pravilen del, tj. ima obliko (23) in torej , je Taylor. Lahko vidimo, da ima za z -* z0 funkcija /(r) mejno vrednost: Izrek 17. Izolirana singularna točka zq funkcije f(z) je odstranljiva, če in samo če je funkcija J(z) omejeno v neki preluknjani okolici točke zq, Zgmechai ne. Naj bo r0 odstranljiva singularna točka f(r). Ob predpostavki, da dobimo, da je funkcija f(r) analitična v nekem krogu s središčem v točki th. To določa ime točke - za enkratno uporabo. Izrek 18. Izolirana singularna točka zq funkcije f(z) je pol, če in samo če glavni del Laurentove ekspanzije funkcije f(z) v okolici točke vsebuje končno (in pozitivno) število neničelnih členov, tj. ima obliko 4 Naj bo z0 pol. Od takrat obstaja preluknjana okolica točke z0, v kateri je funkcija f(z) analitična in različna od nič. Nato je v tej okolici definirana analitična funkcija in zato je točka zq odstranljiva singularna točka (ničla) funkcije ali kjer je h(z) analitična funkcija, h(z0) ∩ 0. je analitična v okolici točke zq, od koder torej dobimo, da Predpostavimo, da ima funkcija f(z) dekompozicijo oblike (24) v preluknjani okolici točke zo. To pomeni, da je v tej okolici funkcija f(z) analitična skupaj s funkcijo. Za funkcijo g(z) velja razširitev, iz katere je razvidno, da je zq odstranljiva singularna točka funkcije g(z) in obstaja. Potem funkcija teži k 0 - pol funkcije. Obstaja še en preprost dejstvo. Točka Zq je pol funkcije f(z), če in samo če je funkcijo g(z) = y mogoče razširiti na analitično funkcijo v okolici točke zq z nastavitvijo g(z0) = 0. Vrstni red pola funkcije f(z) imenujemo ničelni red funkcije jfa. Izreka 16 in 18 implicirata naslednjo trditev. Izrek 19. Izolirana singularna tanka je v bistvu singularna, če in samo če glavni del Laurentove ekspanzije v preluknjani okolici te točke vsebuje neskončno veliko členov, ki niso nič. Primer 5. Singularna točka funkcije je zo = 0. Imamo izolirane singularne točke Laurentove serije in njihovo klasifikacijo. Zato je zo = 0 odstranljiva singularna točka. Razširitev funkcije /(z) v Laurentovo vrsto v okolici ničelne točke vsebuje le pravilen del: Primer7. f(z) = Singularna točka funkcije f(z) je zq = 0. Upoštevajte obnašanje te funkcije na realni in imaginarni osi: na realni osi pri x 0, na imaginarni osi. Zato niti končna niti neskončna meja f(z) pri z -* 0 ne obstaja. Zato je točka r0 = 0 v bistvu singularna točka funkcije f(z). Poiščimo Laurentovo ekspanzijo funkcije f(z) v okolici ničelne točke. Za vsak kompleks C imamo nastavljeno We. Nato Laurentova razširitev vsebuje neskončno število členov z negativnimi potencami z.

Modeli, ki jih opisujejo sistemi dveh avtonomnih diferencialnih enačb.

fazna ravnina. Fazni portret. izoklina metoda. glavne izokline. Stabilnost stabilnega stanja. Linearni sistemi. Tipi ključnih točk: vozlišče, sedlo, žarišče, središče. Primer: kemijske reakcije prvega reda.

Najbolj zanimive rezultate pri kvalitativnem modeliranju lastnosti bioloških sistemov smo dobili na modelih dveh diferencialnih enačb, ki omogočata kvalitativno študijo z metodo fazna ravnina. Razmislite o sistemu dveh avtonomnih navadnih diferencialnih enačb splošne oblike

(4.1)

P(x,y), Q(x,y)- zvezne funkcije definirane v neki domeni G Evklidska ravnina ( x,y- kartezične koordinate) in imajo v tem območju zvezne odvodnice reda, ki ni nižji od prvega.

Regija G je lahko neomejeno ali omejeno. Če spremenljivke x, y imajo določen biološki pomen (koncentracije snovi, številčnost vrst), največkrat območje G je pozitivni kvadrant desne polravnine:

0 £ x< ¥ ,0 £ l< ¥ .

Koncentracije snovi ali številčnost vrst se lahko omejijo tudi od zgoraj z volumnom posode ali s površino habitata. Potem ima obseg spremenljivk obliko:

0 £ x< x 0 , 0 £ l< y 0 .

Spremenljivke x, y sprememba časa v skladu s sistemom enačb (4.1), tako da vsako stanje sistema ustreza paru vrednosti spremenljivk ( x, y).

Nasprotno pa za vsak par spremenljivk ( x, y) ustreza določenemu stanju sistema.

Razmislite o ravnini s koordinatnimi osmi, na kateri so narisane vrednosti spremenljivk x,y. Vsaka točka M ta ravnina ustreza določenemu stanju sistema. Takšno ravnino imenujemo fazna ravnina in prikazuje celoto vseh stanj sistema. Točko M(x, y) imenujemo upodabljajoča ali upodabljajoča točka.

Naj na začetku t=t 0 predstavlja koordinate točke M 0 (x(t 0),y(t 0)). V vsakem naslednjem trenutku v času t upodobitvena točka se bo premaknila glede na spremembe vrednosti spremenljivk x(t),y(t). Niz točk M(x(t), y(t)) na fazni ravnini, katere položaj ustreza stanjem sistema v procesu spreminjanja spremenljivk skozi čas x(t), y(t) po enačbah (4.1) imenujemo fazna trajektorija.

Niz faznih trajektorij za različne začetne vrednosti spremenljivk daje lahko viden "portret" sistema. Stavba fazni portret omogoča sklepanje o naravi sprememb spremenljivk x, y brez poznavanja analitičnih rešitev izvirnega sistema enačb(4.1).

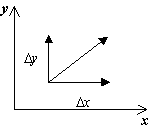
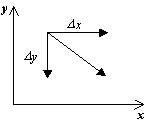
Za upodobitev faznega portreta je potrebno zgraditi vektorsko polje smeri za trajektorije sistema v vsaki točki fazne ravnine. Z določitvijo prirastkaD t>0,dobimo ustrezne prirastke D x in D l iz izrazov:

D x=P(x,y)D t,

D y=Q(x,y)D t.

smer vektorja dy/dx na točki ( x, y) odvisno od predznaka funkcij P(x, y), Q(x, y) in se lahko poda s tabelo:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Rešitev te enačbe y=y(x, c), ali implicitno F(x,y)=c, Kje z je konstanta integracije, daje družino integralnih krivulj enačbe (4.2) - fazne trajektorije sistem (4.1) na ravnini x, y.

Izoklinska metoda

Za izdelavo faznega portreta se uporablja izoklinska metoda - Na fazni ravnini so narisane črte, ki sekajo integralne krivulje pod enim določenim kotom. Enačbo izokline je enostavno dobiti iz (4.2). Postavimo

Kje A– določena konstanta. Pomen A predstavlja tangento naklona tangente na fazno trajektorijo in lahko sprejme vrednosti od -¥ na + ¥ . Zamenjava namesto dy/dx v (4.2) količino A dobimo enačbo izokline:

.(4.3)

Enačba (4.3) določa v vsaki točki ravnine edino tangento na ustrezno integralno krivuljo, razen točke, kjer P(x,y)= 0, Q (x,y) = 0 , pri kateri postane smer tangente nedoločena, saj vrednost odvoda postane nedoločena:

.

Ta točka je presečišče vseh izoklin - posebna točka. Hkrati izniči časovne odvode spremenljivk x in l.

Tako so v singularni točki stopnje spreminjanja spremenljivk enake nič. Zato singularna točka diferencialnih enačb faznih trajektorij (4.2) ustreza stacionarno stanje sistema(4.1), njegove koordinate pa so stacionarne vrednosti spremenljivk x, y.

Posebej zanimivi so glavne izokline:

dy/dx=0, P(x,y)=0 – izoklina vodoravnih tangent in

dy/dx=¥ , Q(x,y)=0 – izoklina navpičnih tangent.

Z izgradnjo glavnih izoklin in iskanjem njihovega presečišča (x,y), katere koordinate izpolnjujejo pogoje:

tako bomo našli presečišče vseh izoklin fazne ravnine, v kateri je smer tangent na fazne trajektorije nedoločena. to - singularna točka, kar ustreza stacionarno stanje sistema(slika 4.2).

Sistem (4.1) ima toliko stacionarnih stanj, kolikor je presečišč glavnih izoklin na fazni ravnini.

Vsaka fazna trajektorija ustreza nizu gibanj dinamičnega sistema, ki prehajajo skozi ista stanja in se med seboj razlikujejo le po začetku referenčnega časa.

Če so izpolnjeni pogoji Cauchyjevega izreka, potem skozi vsako točko prostora x, y, t poteka skozi eno samo integralno krivuljo. Enako velja zahvaljujoč avtonomiji za fazne trajektorije: edinstvena fazna trajektorija poteka skozi vsako točko fazne ravnine.

Stabilnost stabilnega stanja

Naj bo sistem v ravnovesju.

Potem se reprezentativna točka nahaja na eni od singularnih točk sistema, v kateri je po definiciji:

.

Ali je singularna točka stabilna ali ne, je odvisno od tega, ali reprezentativna točka zapusti ali ne z majhnim odstopanjem od stacionarnega stanja. Kot se uporablja za sistem dveh enačb, definicija stabilnosti v jezikue, dkot sledi.

Ravnotežno stanje je stabilno, če za katero koli dano območje obstajajo odstopanja od ravnotežnega stanja (e )območje je mogoče določiti d (e ), ki obdaja stanje ravnovesja in ima to lastnost, da ni poti, ki se začne znotraj regije d , ne bo nikoli dosegel meje e . (slika 4.4)

Za velik razred sistemov - grobi sistemi – katerih narava obnašanja se ne spremeni z majhno spremembo vrste enačb, lahko informacije o vrsti obnašanja v bližini stacionarnega stanja pridobimo s preučevanjem ne izvirnika, ampak poenostavljenega linearizirano sistem.

Linearni sistemi.

Razmislite o sistemu dveh linearnih enačb:

.(4.4)

Tukaj a, b, c, d- konstante, x, y- Kartezične koordinate na fazni ravnini.

Splošno rešitev bomo iskali v obliki:

.(4.5)

Nadomestite te izraze v (4.4) in zmanjšajte za e l t:

(4.6)

Algebraični sistem enačb (4.6) z neznankami A, B ima neničelno rešitev le, če je njena determinanta, sestavljena iz koeficientov neznank, enaka nič:

.

Če razširimo to determinanto, dobimo značilno enačbo sistema:

.(4.7)

Rešitev te enačbe daje vrednosti indikatorjal 1,2 , pod katerim so možne neničelne vrednosti za A in B rešitve enačbe (4.6). Te vrednosti so

.(4.8)

Če je radikalni izraz negativen, poteml 1,2 kompleksna konjugirana števila. Predpostavimo, da imata oba korena enačbe (4.7) neničelne realne dele in da ni več korenin. Potem lahko splošno rešitev sistema (4.4) predstavimo kot linearno kombinacijo eksponentov z eksponentil 1 , l 2 :

(4.9)

Za analizo narave možnih trajektorij sistema na fazni ravnini uporabljamo linearna homogena transformacija koordinat, ki bo sistem pripeljal do kanonična oblika:

,(4.10)

ki omogoča bolj priročno predstavitev na fazni ravnini v primerjavi z originalnim sistemom (4.4). Predstavimo nove koordinateξ , η po formulah:

(4.1)

Iz tečaja linearne algebre je znano, da če realni deli niso enaki ničl 1 , l 2 originalni sistem (4.4) s pomočjo transformacij (4.11) lahko vedno transformiramo v kanonično obliko (4.10) in proučujemo njegovo obnašanje na fazni ravniniξ , η . Razmislite o različnih primerih, ki se lahko pojavijo tukaj.

Korenine λ 1 , λ 2 – veljaven in istega znaka

V tem primeru so transformacijski koeficienti realni, premikamo se iz realne ravninex,yna realno ravnino ξ, η. Če drugo od enačb (4.10) delimo s prvo, dobimo:

.(4.12)

Z integracijo te enačbe ugotovimo:

Kje .(4.13)

Dogovorimo se, da razumemo z λ 2 koren karakteristične enačbe z velikim modulom, ki ne krši splošnosti našega razmišljanja. Potem, ker so v obravnavanem primeru korenine λ 1 , λ2 – veljavna in istega znaka,a>1 , in imamo opravka z integralnimi krivuljami paraboličnega tipa.

Vse integralne krivulje (razen osi η , kar ustreza ) se dotikajo v izhodišču osi ξ, ki je tudi integralna krivulja enačbe (4.11). Izhodišče koordinat je singularna točka.

Ugotovimo zdaj smer gibanja reprezentativne točke vzdolž faznih trajektorij. Če je λ 1, λ 2 negativni, potem je, kot je razvidno iz enačb (4.10), |ξ|, |η| sčasoma zmanjšati. Predstavljajoča točka se približa izvoru, vendar ga nikoli ne doseže. V nasprotnem primeru bi bilo to v nasprotju s Cauchyjevim izrekom, ki pravi, da poteka samo ena fazna trajektorija skozi vsako točko fazne ravnine.

Takšna singularna točka, skozi katero gredo integralne krivulje, tako kot družina parabol poteka skozi izvor, se imenuje vozlišče (sl. 4.5)

Ravnotežno stanje tipa vozla pri λ 1, λ 2 < 0 je po Ljapunovu stabilen, saj se predstavna točka giblje po vseh integralnih krivuljah proti izhodišču koordinat. to stabilen vozel. Če je λ 1, λ 2 > 0, torej |ξ|, |η| narašča s časom in reprezentativna točka se odmika od izhodišča. V tem primeru singularna točka– nestabilno vozlišče .

Na fazni ravnini x, y splošni kvalitativni značaj obnašanja integralnih krivulj bo ostal, vendar tangente na integralne krivulje ne bodo sovpadale s koordinatnimi osemi. Kot naklona teh tangent bo določen z razmerjem koeficientov α , β , γ , δ v enačbah (4.11).

Korenine λ 1 , λ 2 so veljavni in imajo različne znake.

Pretvori iz koordinate x,y na koordinate ξ, η spet resnično. Enačbe za kanonične spremenljivke imajo spet obliko (4.10), vendar so zdaj predznaki λ 1, λ 2 drugačen. Enačba fazne trajektorije ima obliko:

Kje ,(4.14)

Z integracijo (4.14) ugotovimo

(4.15)

to enačba določa družino krivulj hiperboličnega tipa, kjer sta obe koordinatni osi so asimptote (at a=1 imeli bi družino enakokrakih hiperbol). Tudi koordinatne osi so v tem primeru integralne krivulje– to bodo edine integralne krivulje, ki potekajo skozi izhodišče. Vsakki je sestavljen iz treh faznih trajektorij: dveh gibanj proti stanju ravnotežja (ali stran od stanja ravnovesja) in iz stanja ravnovesja. Vse druge integralne krivulje– so hiperbole, ki ne potekajo skozi izhodišče (sl. 4.6) Ta singularna točka se imenuje "sedlo ». Niveletne črte v bližini gorskega sedla se v bližini sedla obnašajo kot fazne trajektorije.

Oglejmo si naravo gibanja reprezentativne točke vzdolž faznih trajektorij blizu ravnotežnega stanja. Naj npr.λ 1 >0, λ 2<0 . Nato je reprezentativna točka postavljena na os ξ , se bo odmaknila od izhodišča in postavila na os η – se bo neomejeno približevalo izhodišču koordinat, ne da bi ga dosegli v končnem času. Kjerkoli je reprezentančna točka v začetnem trenutku (z izjemo singularne točke in točk na asimptoti η =0), sčasoma se bo odmaknila od ravnotežnega stanja, tudi če se bo na začetku pomikala po eni od integralnih krivulj proti singularni točki.

To je očitno singularna točka tipa sedla je vedno nestabilna . Samo pri posebej izbranih začetnih pogojih na asimptotiη =0 sistem se bo približal stanju ravnovesja. Vendar to ni v nasprotju s trditvijo, da je sistem nestabilen. Če štejete, da so vsa začetna stanja sistema na fazni ravnini enako verjetna, potem je verjetnost takega začetnega stanja, ki ustreza gibanju v smeri Za singularna točka je enaka nič. Zato bo vsak realni premik sistem odstranil iz stanja ravnovesja.Če se vrnem k koordinatamx,y,dobimo enako kvalitativno sliko narave gibanja trajektorij okoli izhodišča.

Meja med obravnavanima primeroma vozlišča in sedla je primer Kdaj eden od značilnih indikatorjev, npr λ 1 , izgine, kar se zgodi, ko determinanta sistema- izražanje adbc=0(glej formulo 4.8 ). V tem primeru so koeficienti desnih strani enačb (4.4) sorazmerni drug z drugim:

in sistem ima za svoja ravnotežna stanja vse točke premice:

Preostale integralne krivulje so družina vzporednih premic z naklonom , po katerem se reprezentativne točke bodisi približajo ravnotežnemu stanju bodisi oddaljijo od njega, odvisno od predznaka drugega korena karakteristične enačbe λ 2 = a+d.(slika 4. 7 ) V tem primeru so koordinate ravnotežnega stanja odvisne od začetne vrednosti spremenljivk.

Korenine λ 1 , λ 2 – kompleksenkonjugat

V tem primeru zaresx in l bomo imajo kompleksne konjugate ξ , η (4.10) . Z uvedbo še ene vmesne transformacije pa je tudi v tem primeru mogoče zmanjšati obravnavo na pravo linearno homogeno transformacijo. Postavimo:

(4.16)

Kje a, b, in u, v – prave vrednosti. Lahko se pokaže, da je transformacija izx,y Za u, v je pod našimi predpostavkami realna, linearna, homogena z determinanto, ki ni nič. Zaradi enačb(4.10, 4.16) imamo:

kje

(4.17)

Delitev druge enačbe s prvo, dobimo:

kar je lažje integrirati, če preidemo na polarni koordinatni sistem (r, φ ) . Po zamenjavi od kje dobimo:

.(4.18)

Tako na fazni ravniniu, vimamo opravka z družino logaritemskih spiral, od katerih ima vsakaasimptotična točka v izhodišču.Singularna točka, ki je asimptotična točka vseh integralnih krivulj, ki imajo obliko spiral, ugnezdeni prijatelj vprijatelj, poklical fokus ( sl.4.8 ) .

Razmislimo o naravi gibanja predstavitvene točke vzdolž faznih trajektorij. Množenje prve od enačb (4.17) zu, drugi pa do v in če dodamo, dobimo:

Kje

Pustiti a 1 < 0 (a 1 = Reλ ) . Predstavljajoča točka se nato nenehno približuje izvoru, ne da bi ga dosegla v končnem času. To pomeni, da so fazne trajektorije zasukane spirale in ustrezajo dušenim nihanjem spremenljivke. to - enakomeren fokus .

V primeru stabilnega žarišča, tako kot v primeru stabilnega vozla, ni izpolnjen le pogoj Lyapunov, ampak tudi strožja zahteva. Namreč, za morebitna začetna odstopanja se bo sistem sčasoma vrnil čim bližje želenemu ravnotežnemu položaju. Takšna stabilnost, pri kateri se začetna odstopanja ne samo ne povečujejo, ampak upadajo, težijo k ničli, se imenuje absolutna stabilnost .

Če je v formuli (4.18) a 1 >0 , potem se točka, ki predstavlja, odmakne od izhodišča in imamo opravka z nestabilen fokus . Pri premikanju iz letalau, vna fazno ravninox, ltudi spirale bodo ostale spirale, a bodo deformirane.

Razmislite zdaj o primeru, koa 1 =0 . Fazne trajektorije na ravniniu, vbodo krogi ki na letalux,yfit elipse:

Tako pria 1=0 skozi posebno točkox= 0,y= 0 nobena integralna krivulja ne poteka. Tako izolirano singularno točko, v bližini katere so integralne krivulje zaprte krivulje, zlasti elipse, vložene druga v drugo in obdajajo singularno točko, imenujemo središče.

Možnih je torej šest vrst ravnovesja, odvisno od narave korenov karakteristične enačbe (4.7). Pogled na fazne trajektorije na ravnini x, y za teh šest primerov je prikazano na sl. 4.9.

riž. 4.9.Vrste faznih portretov v okolici stacionarnega stanja za sistem linearnih enačb (4.4).

Pet vrst ravnotežnih stanj je grobih, njihova narava se ne spremeni z dovolj majhnimi spremembami na desni strani enačb (4.4). V tem primeru bi morale biti spremembe majhne ne samo v desnih straneh, ampak tudi v njihovih odvodih prvega reda. Šesto stanje ravnovesja - središče - ni grobo. Z majhnimi spremembami parametrov desne strani enačb gre v stabilen ali nestabilen fokus.

Bifurkacijski diagram

Naj uvedemo zapis:

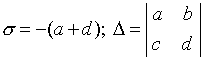. (4.11)

Potem lahko značilno enačbo zapišemo v obliki:

. (4.12)

Razmislite o ravnini s pravokotnimi kartezičnimi koordinatami s , D in na njem označite območja, ki ustrezajo eni ali drugi vrsti ravnotežnega stanja, ki je določena z naravo korenin značilne enačbe

.(4.13)

Pogoj za stabilnost ravnotežnega stanja bo prisotnost negativnega realnega dela yl 1 in l 2 . Nujen in zadosten pogoj za to je izpolnjevanje neenakostis > 0, D > 0 . Na diagramu (4.15) ta pogoj ustreza točkam, ki se nahajajo v prvi četrtini ravnine parametrov. Singularna točka bo fokus, čel 1 in l 2 kompleksen. Ta pogoj ustreza tistim točkam ravnine, za katere , tiste. točke med dvema vejama paraboles 2 = 4 D. Točke polose s = 0, D>0, ustrezajo ravnotežnim stanjem središčnega tipa. prav takol 1 in l 2 - veljavni, vendar različni znaki, tj. singularna točka bo sedlo, če D<0, itd. Kot rezultat dobimo razdelilni diagram ravnine parametrov s, D, v območja, ki ustrezajo različnim vrstam ravnotežnih stanj.

riž. 4.10. Bifurkacijski diagram

za sistem linearnih enačb 4.4

Če so koeficienti linearnega sistema a, b, c, d odvisno od nekega parametra, potem ko se ta parameter spremeni, se bodo spremenile tudi vrednostis , D . Pri prehodu skozi meje se narava faznega portreta kvalitativno spremeni. Zato se takšne meje imenujejo bifurkacijske meje - na nasprotnih straneh meje ima sistem dva topološko različna fazna portreta in temu primerno dva različna tipa obnašanja.

Diagram prikazuje, kako lahko pride do takšnih sprememb. Če izključimo posebne primere - izvor koordinat - potem je lahko videti, da lahko sedlo preide v vozlišče, stabilno ali nestabilno, ko prečka os y. Stabilno vozlišče se lahko premakne na sedlo ali stabilen fokus itd. Upoštevajte, da prehodi stabilno vozlišče–stabilen fokus in nestabilno vozlišče–nestabilen fokus niso bifurkacijski, saj se topologija faznega prostora v tem primeru ne spremeni. O topologiji faznega prostora in bifurkacijskih prehodih bomo podrobneje govorili v 6. predavanju.

Pri bifurkacijskih prehodih se spremeni narava stabilnosti singularne točke. Na primer, stabilno ostrenje skozi sredino se lahko spremeni v nestabilno ostrenje. Ta bifurkacija se imenuje Andronov-Hopfova bifurkacija po imenih znanstvenikov, ki so ga preučevali. S to bifurkacijo se v nelinearnih sistemih rodi mejni cikel in sistem postane samonihalen (glej predavanje 8).

Primer. Sistem linearnih kemijskih reakcij

Snov X teče od zunaj s konstantno hitrostjo, se spremeni v snov Y in s hitrostjo, ki je sorazmerna koncentraciji snovi Y, se vzame iz reakcijske sfere. Vse reakcije so prvega reda, z izjemo dotoka snovi od zunaj, ki ima ničelni red. Reakcijska shema izgleda takole:

(4.14)

in je opisan s sistemom enačb:

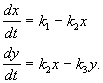(4.15)

Stacionarne koncentracije dobimo tako, da desne strani enačimo z nič:

.(4.16)

Razmislite o faznem portretu sistema. Razdelimo drugo enačbo sistema (4.16) s prvo. Dobimo:

.(4.17)

Enačba (4.17) določa obnašanje spremenljivk na fazni ravnini. Izdelajmo fazni portret tega sistema. Najprej na fazno ravnino narišemo glavne izokline. Enačba izokline navpičnih tangent:

Enačba za izoklino vodoravnih tangent:

Singularna točka (stacionarno stanje) leži na presečišču glavnih izoklin.

Zdaj pa ugotovimo, pod kakšnim kotom koordinatne osi sekajo integralne krivulje.

če x= 0, potem.

Tako je tangenta naklona tangente na integralne krivulje y=y(x), prečkajo os y x=0, je negativna v zgornji polravnini (spomnimo se, da spremenljivke x, y imajo vrednosti koncentracije, zato nas zanima samo zgornji desni kvadrant fazne ravnine). V tem primeru se vrednost tangenta kota naklona tangente povečuje z oddaljenostjo od izhodišča.

Razmislite o osi y= 0. V presečišču te osi so integralne krivulje opisane z enačbo

pri tangens naklona integralnih krivulj, ki prečkajo abscisno os, je pozitiven in z naraščanjem narašča od nič do neskončnosti x.

Ob .

Nato se z nadaljnjim povečevanjem tangenta naklona zmanjša v absolutni vrednosti, ostane negativna in se nagiba k -1 pri x ® ¥ . Če poznamo smer tangent na integralne krivulje na glavnih izoklinah in na koordinatnih oseh, je enostavno zgraditi celotno sliko faznih trajektorij.

Naravo stabilnosti singularne točke bomo ugotavljali z metodo Lyapunova. Značilna determinanta sistema ima obliko:

.

Z razširitvijo determinante dobimo značilno enačbo sistema: , tj. oba korena karakteristične enačbe sta negativna. Zato je stacionarno stanje sistema stabilno vozlišče. Hkrati koncentracija snovi X teži k stacionarnemu stanju vedno monotono, koncentracija snovi Y lahko prehaja čez min ali max. Oscilacijski režimi v takem sistemu so nemogoči.

Opredelitev. Singularna točka funkcije se imenuje izoliran, če je v neki okolici te točke analitična funkcija (to je analitična v obroču).

Klasifikacija izoliranih singularnih točk funkcije je povezana z obnašanjem te funkcije v okolici singularne točke.

Opredelitev. Točka se imenuje za enkratno uporabo singularna točka funkcije, če obstaja končna meja te funkcije pri .

Primer 5 Pokažite, da ima funkcija v točki odstranljivo singularnost.

rešitev.Če se spomnimo prve izjemne meje, izračunamo

To pomeni, da ima dana funkcija v točki odstranljivo singularnost.

Naloga 4. Pokažite, da je točka odstranljiva za .

Opredelitev. Točka se imenuje palica funkcija , če ta funkcija neomejeno narašča za , to je .

Bodimo pozorni na povezavo med pojmoma ničle in pola analitične funkcije. Predstavimo funkcijo kot.

Če je točka preprosta ničla funkcije, potem ima funkcija preprost pol

Če je točka ničelni red za funkcijo, potem je to za funkcijo pol naročilo.

Primer 6 Pokažite, da ima funkcija pol tretjega reda v točki.

rešitev. Ob predpostavki dobimo. Ker težimo k ničli, imamo po katerem koli zakonu . Potem , in s tem tudi sama funkcija neomejeno narašča. Zato je , to je singularna točka pol. Za funkcijo je ta točka očitno trojna ničla. Zato je za to funkcijo točka pol tretjega reda.

Naloga 5. Pokažite, da ima točka preprost pol.

Opredelitev. Točka se imenuje v bistvu posebnega točka funkcije, če na tej točki ni niti končne niti neskončne meje funkcije (vedenje funkcije ni definirano).

Pustiti je bistvena singularna točka funkcije . Potem za poljubno vnaprej dodeljeno kompleksno število obstaja takšno zaporedje točk, ki konvergira k , vzdolž katerega vrednosti težijo k : ( Sochockijev izrek).

Primer 7 Pokažite, da ima funkcija v točki bistveno singularnost.

rešitev. Razmislite o obnašanju dane funkcije v bližini točke. Za vzdolž pozitivnega dela realne osi (tj. ) imamo in ; če vzdolž negativnega dela realne osi (tj.), potem in . Torej ni omejitev za. Po definiciji ima funkcija bistveno singularnost v točki.

Oglejmo si obnašanje funkcije na ničli z vidika Sochockijevega izreka. Naj bo poljubno kompleksno število, razen nič in neskončnosti.

Iz enakosti ugotovimo. Ob predpostavki dobimo zaporedje točk , . Očitno,. V vsaki točki tega zaporedja je funkcija enaka , in zato

Naloga 6. Pokažite, da ima funkcija bistveno singularnost v točki.

Točka v neskončnosti se vedno šteje za posebno za funkcijo. Točka se imenuje izolirana singularna točka funkcije, če ta funkcija nima drugih singularnih točk zunaj nekega kroga s središčem v izhodišču.

Razvrstitev izoliranih singularnih točk lahko razširimo tudi na primer .

Primer 8 Pokažite, da ima funkcija dvojni pol v neskončnosti.

rešitev. Upoštevajte funkcijo , kjer je analitična funkcija v okolici točke in . To pomeni, da ima funkcija dvojno ničlo v neskončnosti, vendar je potem za funkcijo točka dvojni pol.

Primer 9 Pokažite, da ima funkcija bistveno singularnost v neskončnosti.

rešitev. Podoben problem je obravnavan v pr.7. Razmislite o obnašanju funkcije v okolici neskončno oddaljene točke. Za vzdolž pozitivnega dela realne osi in za negativni del realne osi. To pomeni, da v točki ni omejitve funkcije in je na podlagi definicije ta točka v bistvu singularna.

Naravo singularnosti funkcije v točki lahko presojamo iz glavni del Laurentova širitev v bližini te točke.

1. izrek. Da bo bistvo za enkratno uporabo singularna točka funkcije , je nujno in zadostno, da ustrezna Laurentova ekspanzija ni vseboval glavnega dela.

Naloga 6. Z uporabo Taylorjevega raztezanja funkcije v okolici točke pokažite, da ima na ničli odstranljivo singularnost.

2. izrek. Da bo bistvo palica funkcij , je potrebno in zadostuje, da glavni del ustrezna Laurentova razširitev vsebovalo končno število članov :

Število najvišjega negativnega člena določa vrstni red pola.

V tem primeru lahko funkcijo predstavimo kot

kjer je funkcija, analitična v točki, je vrstni red pola.

Primer 10 Pokažite, da ima funkcija enostavne poli v točkah.

rešitev. Razmislimo o točki. Uporabimo Laurentovo razširitev te funkcije v bližini te točke, pridobljeno v primeru 2:

Ker je največja (in edina) negativna potenca v glavnem delu te ekspanzije enaka ena, je točka preprost pol te funkcije.

Ta rezultat bi lahko dosegli tudi drugače. Predstavimo v obliki in postavimo - to je funkcija, ki je analitična v točki in . Zato ima ta funkcija zaradi (8) preprost pol v točki.

Drug način: razmislite o funkciji, ki ima na točki preprosto ničlo. Zato ima na tej točki preprost pol.

Podobno, če funkcijo zapišemo v obliki , kjer je funkcija analitična v točki in , potem je takoj jasno, da je točka preprost pol funkcije .

Naloga 7. Pokažite, da ima funkcija pol 2. reda v točki in pol 4. reda v točki .

Izrek 3. Da bo bistvo v bistvu posebnega točka funkcije , je nujno in zadostno, da glavni del Laurentova širitev v bližini točke vsebovalo neskončno število članov .

Primer 11. Določite naravo singularnosti v točki funkcije

rešitev. Pri dobro znani ekspanziji kosinusa namesto:

Zato ima Laurentova ekspanzija v okolici točke obliko

Tukaj je pravilen del en izraz. In glavni del vsebuje neskončno število členov, tako da je točka v bistvu singularna.

Naloga 8. Pokažite, da ima funkcija v točki bistveno singularnost.

Razmislite o neki funkciji in zapišite njeno Laurentovo razširitev na točki:

Naredimo zamenjavo, medtem ko gre točka na točko. Zdaj, v okolici točke v neskončnosti, imamo

Ostaja še uvedba novega poimenovanja. Dobimo

kjer je glavni del in je regularni del Laurentove ekspanzije funkcije v okolici neskončno oddaljene točke. Tako je pri Laurentovi ekspanziji funkcije v okolici točke glavni del niz v pozitivnih potencah, medtem ko je pravilen del niz v negativnih potencah. Ob upoštevanju tega

Zgornja merila za določitev narave singularnosti pa ostajajo veljavna za neskončno oddaljeno točko.

Primer 12. Ugotovite naravo singularnosti funkcije v točki. , potem se lahko na neki točki izkaže, da ni izoliran.

Primer 15 Funkcija v neskončno oddaljeni točki ima bistveno singularnost. Pokažite, da točka funkcije ni izolirana singularna točka.

rešitev. Funkcija ima neskončno število polov na ničlah imenovalca, to je v točkah , . Ker , Potem je točka , V kateri koli okolici, katere so poli, mejna točka za poli.

singularna točka

v matematiki.

1) Singularna točka krivulje, podana z enačbo F ( x, y) = 0, - točka M 0 ( x 0, y 0), v kateri sta oba delna odvoda funkcije F ( x, y) izgine:

Če poleg tega niso vsi drugi delni odvodi funkcije F ( x, y) v točki M 0 enaki nič, potem se O. t. imenuje dvojno. Če skupaj z izničenjem prvih odvodov v točki M 0 izginejo vsi drugi odvodi, vendar niso vsi tretji odvodi enaki nič, se O. t. imenuje trojni itd. Pri preučevanju strukture krivulje v bližini dvojnega O. t. igra pomembno vlogo znak izraza

Če je Δ > 0, se O. t. imenuje izoliran; na primer krivulja y 2 - x 4 + 4x 2= 0 je izvor izoliran O. t. (glej riž. 1 ). Če je Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 je izvor koordinat vozlišče O. t. (glej riž. 2 ). Če je Δ = 0, je O. t. krivulja bodisi izolirana bodisi označena z dejstvom, da imajo različne veje krivulje na tej točki skupno tangento, na primer: tangento in tvorijo točko, kot je krivulja y 2 - x 3= 0 (glej riž. 3 , a); b) vrh 2. vrste - različne veje krivulje se nahajajo na isti strani skupne tangente, kot krivulja (y - x 2)2 - x 5= 0 (glej riž. 3 , b); c) točka samostika (za krivuljo y 2 - x 4= 0 izvor je točka samostika; (cm. riž. 3 , V). Poleg navedenega O. t. obstajajo številni drugi O. t. s posebnimi imeni; na primer, asimptotična točka je vrh spirale z neskončnim številom obratov (glej sl. riž. 4 ), prelomna točka, kotna točka itd.

2) Singularna točka diferencialne enačbe je točka, v kateri števec in imenovalec desne strani diferencialne enačbe istočasno izničita (glej Diferencialne enačbe)

kjer sta P in Q zvezno diferencibilni funkciji. Ob predpostavki, da se O. t. nahaja v izhodišču koordinat in uporabimo Taylorjevo formulo (glej Taylorjevo formulo), lahko enačbo (1) predstavimo v obliki

kjer je P 1 ( x, y) in Q 1 ( x, y) so neskončno majhne glede na

Namreč, če je λ 1 ≠ λ 2 in λ 1 λ 2 > 0 ali λ 1 = λ 2, potem je O. t. vanj vstopijo vse integralne krivulje, ki potekajo skozi točke dovolj majhne okolice vozlišča. Če je λ 1 ≠ λ 2 in λ 1 λ 2 i β, α ≠ 0 in β ≠ 0, potem je O. t. vse integralne krivulje, ki potekajo skozi točke v dovolj majhni okolici žarišča, so spirale z neskončnim številom obratov v poljubno majhni okolici žarišča. Če je končno λ 1,2 = ± jazβ, β ≠ 0, potem značaj O. t. ni določen z linearnimi členi v razširitvah P ( x, y) in Q ( x, y), kot je bilo v vseh zgornjih primerih; tukaj je O. t. lahko žarišče ali središče ali pa ima bolj kompleksen značaj. V okolici središča so vse integralne krivulje zaprte in vsebujejo središče v sebi. Tako je na primer točka (0, 0) vozlišče za enačbe pri" = 2u/x(λ 1 = 1, λ 2 = 2; glej riž. 5 , a) in l" = u/x(λ 1 = λ 2 = 1; glej riž. 5 , b), sedlo za enačbo y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. riž. 6 ), središče za enačbo y" =(x + y) / (x - y) (λ 1 = 1 - jaz, λ 2 = 1 + jaz; cm. riž. 7 ) in središče enačbe y" = -x / y(λ 1 = -jaz, λ 2 = jaz; cm. riž. 8 ).

Če x, y) in Q ( x, y) so analitični, lahko okolico O. t. višjega reda razdelimo na področja: D 1 - zapolnjena z integralnimi krivuljami, oba konca vstopata v O. t. (eliptična območja), D 2 - zapolnjena z integralnimi krivuljami, en konec, ki vstopa v O. t. (parabolične regije), in D 3 - območja, omejena z dvema integralnima krivuljama, vključenima v O. t., med katerimi so integralne krivulje tipa hiperbol (hiperbolične regije) (glej. riž. 9 ). Če v O. točko ne vstopa nobena integralna krivulja, se O. točka imenuje točka stabilnega tipa. Soseska stabilnega O. t. je sestavljena iz zaprtih integralnih krivulj, ki vsebujejo O. t. v sebi, med katerimi se nahajajo spirale (glej sl. riž. 10 ).

Študija O. t. diferencialnih enačb, to je v bistvu študija obnašanja družin integralnih krivulj v bližini O. t. M. Lyapunov a, A. Poincaré in drugi).

3) Singularna točka enovrednotne analitične funkcije je točka, v kateri je porušena analitičnost funkcije (glej Analitične funkcije). Če obstaja soseska O. t. a, brez drugih O. t., potem točka A se imenuje izoliran O. t. Če A je izoliran O.T. in obstaja končen O.T. imenujemo odstranljiv O.T. Z ustrezno spremembo definicije funkcije v točki a (ali jo ponovno definiramo na tej točki, če funkcija na njej sploh ni definirana), in sicer z nastavitvijo f(a)= b, je mogoče doseči a bo postala navadna točka popravljene funkcije. Na primer pika z= 0 je odstranljiv O.T. za funkcijo f 1 ( z) = f(z), če z≠ 0 in f 1(0),=1, pika z= 0 je navadna točka [ f 1 (z) je v bistvu analitičen z= 0]. če A- izoliran O. t. in a se imenuje pol ali nebistvena singularna točka funkcije f(z), če deluje Laurentova serija). f(z) v soseščini izoliranega O. t. ne vsebuje negativnih moči z - a, Če A- odstranljiv O. t., vsebuje končno število negativnih moči z - a, Če A- drog (v tem primeru vrstni red pola R je definirana kot najvišja potenca a - v bistvu singularne točke. Na primer za funkcijo

p = 2, 3, …)

pika z= 0 je pol reda R, za funkcijo

pika z= 0 je bistvena singularna točka.

Na meji konvergenčnega kroga potenčne vrste mora biti vsaj ena O. t. funkcije, ki jo znotraj tega kroga predstavlja dana potenčna vrsta. Vse mejne točke področja obstoja enovrednostne analitične funkcije (naravna meja) so mejne točke te funkcije. Tako so vse točke enotskega kroga | z| = 1 so posebni za funkcijo

Za večvredno analitično funkcijo je koncept "O. T." težje. Poleg O. t. je v posameznih listih Riemannove ploskve funkcije (to je O. t. enovrednih analitičnih elementov) vsaka vejna točka tudi O. t. funkcije. Izolirane razvejne točke Riemannove ploskve (tj. razvejne točke, tako da v nekaterih njihovih soseščinah ni drugih funkcij O.t. v nobenem listu) so razvrščene kot sledi. Če je a izolirana razvejna točka končnega reda in obstaja končen a, se imenuje kritični pol. če A je izolirana razvejna točka neskončnega reda in a imenujemo transcendentalna O. t. Vse druge izolirane razvejne točke imenujemo kritične bistveno singularne točke. Primeri: pika z= 0 je navadna kritična točka funkcije f ( z) = dnevnik z in kritična bistvena singularna točka funkcije f (z) = dnevnik grehov z.

Vsak O. t., razen odstranljivega, je ovira za analitično nadaljevanje, tj. Analitično nadaljevanje vzdolž krivulje, ki poteka skozi neodstranljivo O. t., je nemogoče.

Velika sovjetska enciklopedija. - M.: Sovjetska enciklopedija. 1969-1978 .

Oglejte si, kaj je "Special Point" v drugih slovarjih:

Točke tukaj. Glej tudi singularna točka (diferencialne enačbe). Značilnost ali singularnost v matematiki je točka, na kateri matematični objekt (običajno funkcija) ni definiran ali se obnaša nepravilno (na primer točka, na kateri ... ... Wikipedia

Analitična funkcija je točka, kjer so kršeni pogoji analitičnosti. Če je analitična funkcija f(z) definirana v neki okolici točke z0 povsod … Fizična enciklopedija

Analitična funkcija je točka, na kateri je kršena analitičnost funkcije ... Veliki enciklopedični slovar

singularna točka- — [Ya.N. Luginsky, M.S. Fezi Zhilinskaya, Yu.S. Kabirov. English Russian Dictionary of Electrical Engineering and Power Industry, Moskva, 1999] Teme elektrotehnike, osnovni koncepti EN singular point ... Priročnik tehničnega prevajalca

1) OT analitične funkcije f(z) je ovira za analitično nadaljevanje elementa funkcije f(z) kompleksne spremenljivke z po neki poti na ravnini te spremenljivke. Naj bo analitična funkcija f(z) definirana z nekaj ... ... Matematična enciklopedija

Analitična funkcija, točka, kjer je analitičnost funkcije kršena. * * * SINGULARNA TOČKA SINGULARNA TOČKA analitične funkcije, točka, v kateri je kršena analitičnost funkcije ... enciklopedični slovar

singularna točka- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. singularna točka vok. ednina Punkt, m rus. singularna točka, fpranc. točkasti delec, m; točka singulier, m … Automatikos terminų žodynas

Pustiti zq - singularna točka funkcije f(z), t.s. f(z) vendar je na tej točki analitična (zlasti na njej morda ni definirana). Če obstaja taka preluknjana okolica točke zq (tj. množica O z - zq f(z) je torej aliatičen zo klical izolirana singularna točka funkcije f(z). Ta opredelitev je ohranjena tudi v primeru zn = oo, če je jod preluknjana okolica točke zq = oo razume nabor z > jaz - videz nekega kroga s središčem v izhodišču. Z drugimi besedami, singularna točka zq naj bi bil izoliran, če obstaja soseska te točke, v kateri obstajajo druge singularne točke, ki se razlikujejo od zq. Povsod spodaj upoštevamo samo singularne točke enovrednega značaja (funkcija f(z) domnevamo, da je edinstven).

Odvisno od obnašanja funkcije f(z) pri z -> zq Obstajajo tri vrste singularnih točk. Izolirana singularna točka funkcije zq f(z) poklican:

1) odstranljiva singularna točkače obstaja končna meja

2) palicače obstaja omejitev

3) bistvena točka,če f(z) nima niti končne niti neskončne meje za z-> zq.

PRIMER 26.1. Pokažimo, da so vse tri vrste singularnih točk realizirane. Razmislite f(z)= točka zq = 0 je izoliran

singularna točka te funkcije. Z uporabo formule (22.12) dobimo razširitev

iz česar sledi, da obstaja lim fi(z)= 1. Zato je zq = 0

je odstranljiva singularna točka funkcije fi(z).

funkcija f'j(z) =--- ima pol na točki zo= 1 ker

2 r“ X

Razmislite zdaj o funkciji )z(z)= e 1 ^ r in pokažite to zo = O je bistvena singularna točka te funkcije. Pri prizadevanju z na nič vzdolž realne osi, leva in desna meja funkcije f (z) drugačen: lim z 1 / 1 = 0,lim z 1 /* = os. To pomeni,

x->0-0 x->0+O

Kaj f:i(z) nima niti končne niti neskončne meje za 2 -> Oh, tj. zq = 0 je v bistvu singularna točka te funkcije. (Upoštevajte, da glede na točko z-iy na ničlo na funkciji imaginarne osi

sploh nima omejitev.)

Seveda obstajajo tudi neizolirane singularne točke. Na primer. funkcija ima poli v točkah z n = -, p= ±1, ±2,...

torej Zq = 0 je neizolirana singularna točka te funkcije: v kateri koli (poljubno majhni) okolici te točke obstajajo druge singularne točke g str.

Pustiti zo- končna izolirana singularna točka funkcije f(z). Potem f(z) je podobno v neki preluknjani soseski 0 Zo točke zo to sosesko lahko obravnavamo kot obroč z notranjim polmerom r = 0. Po izreku 25.1 je v obravnavani soseski funkcija f(z) lahko razširimo v niz Laurent (25.2). Pokazali bomo, da je obnašanje funkcije za 2 -> zq (tj. tip singularne točke zo) odvisno od oblike glavnega dela razkroja (25.2); ta okoliščina pojasnjuje izvor izraza "glavni del".

IZREK 2G.2. Izolirana singularna točka zo funkcije f(z) je odstranljiva, če in samo če ima Lorapova ekspanzija v preluknjani okolici te točke oid

tiste. je sestavljen samo iz pravilnega dela, in vsi koeficienti glavnega dela so enaki krogli.

Dokaz. 1. Naj zo je odstranljiva singularna točka. Dokažimo, da je Laurentova razširitev funkcije f(z) ima obliko (26.1). Od singularne točke zo odstranljiva, potem obstaja končna meja lim f(z) = A. torej f(z) omejena v neki preluknjani okolici 0 z - zq točke zo, tiste. )(z) za vse z iz te soseske. Vzemite katero koli R. U р /?|, in uporabite formule (25.3) za koeficiente Laurentove vrste:

Za koeficiente glavnega dela ekspanzije n =- 1,-2,... Za take vrednosti p imamo p~n-e 0 pri R-> 0. Ker je vrednost R lahko izberete poljubno majhno, torej gospod~" lahko poljubno majhna. Ker |c t,| ^ g~n in cn nista odvisna od p, potem je cn = 0 za in= - 1, -2,..., kar je bilo treba dokazati.

2. Predpostavimo zdaj, da ima Laurentova ekspanzija obliko (26.1). Vrsta (26.1) je potenčna vrsta in. torej konvergira ne samo v preluknjani, ampak tudi v celotni soseski z-zq vključno s piko zo; njegovo količino S(z) je analitičen za z in S(z) = )(z) ob 0 z - zo R. Zato obstaja končna meja lim )(z)\u003d Pm 5 (r) \u003d 5 (r) - Zato je singularna točka zq

Z->Zo Z-*Zo

za enkratno uporabo. Izrek je dokazan.

Komentiraj. Iz dokaza izreka sledi, da je v preluknjani okolici 0 z - zo odstranljive singularne točke funkcija f(z) sovpada s funkcijo S(r), ki je analitična v celotni okolici z - zo . Torej, če postavimo /(th) = S(zq), potem, ne da bi spremenili vrednosti funkcije f(z) na kateri koli točki preluknjane soseske naredimo to funkcijo analitično v r, tj. »odstranite« funkcijo. To pojasnjuje izraz "odstranljiva singularnost". Naravno je, da take točke obravnavamo kot regularne in ne kot singularne točke funkcije f(z).

Upoštevajte na primer funkcijo

V primeru 26.1 je bilo pokazano, da je Pm (n) = 1. tj. singularna točka

zq = 0 je odstranljiv. Če nastavimo /i(0) = 1, s tem odpravimo singularnost in dobimo funkcijo, ki je analitična v točki zq = 0 (in v celotni ravnini C).

Označimo pole v smislu Laurentovih razširitev.

Izrek 26.3. Izolirana singularna točka Zo funkcije f(z) je pol, če in samo če, ko ima glavni del Laurentove ekspanzije s središčem Zq samo končno število različnih

iz koeficientov nič z n:

Dokaz. 1. Naj zq - pol, tj. lim /( z) = oo.

Dokažimo, da je Laurentova razširitev funkcije f(z) ima obliko (2G.2). Od lim f(z)= oo. potem obstaja preluknjana okolica točke

ki zq. pri čemer f(z) je analitičen in nima ničel. Nato funkcija g(z) = 1 /f(z) bo v tej preluknjani soseski tudi analitičen in lim g(z)= 0. Zato je Zo je za enkratno uporabo *-? *0

singularna točka funkcije g(z). Redefinirajmo g(z) na točki zo, dajanje g(zo)= 0. Potem g(z) postane analitičen v celotni okolici (nepreluknjane) točke z 0 , in z0 bo njegova izolirana ničla. Označimo z n večkratnost (vrstni red) te ničle. Kot je bilo prikazano v §23, v okolici točke zq funkcijo g(z) predstavljiv v obliki (glej (23.2))

in (z$) f 0 in y>(z) je analitičen v neki okolici točke zo- Ker ip(z) neprekinjeno na točki zo in g>(zo) F 0" potem ip(z) tudi v neki okolici te točke nima ničel. Torej funkcija 1 /-p(z) bo tudi v tej soseski analitično in se zato v njej razširi v Taylorjevo vrsto:

Če odpremo oklepaje in spremenimo oznake koeficientov, zadnjo razširitev zapišemo v obliki

kjer je c_jv = 1>o f 0. Tako glavni del Laurentove ekspanzije f(r) vsebuje samo končno število členov; smo prišli do zahtevane enakosti (26.2).

2. Pustimo v preluknjano okolico točke th funkcijo )(z) je predstavljen z Laurentovo razširitvijo (26.2) (v bolj razširjeni obliki glej (26.3)), katere glavni del vsebuje samo končno število členov in z- d" f 0. To moramo dokazati Zq - funkcijski pol f(z). Enakost (26.3) pomnožimo s (G - G o) iV , dobimo funkcijo

Vrsta v (26.4) je potenčna vrsta, ki konvergira k analitični funkciji ne samo v preluknjani, ampak tudi v celotni okolici točke Zq. Zato funkcija h(z) postane analitično v tej soseski, če jo razširimo v th z nastavitvijo h(zo)= s_dg f 0. Potem

Točka o je torej pol in izrek 26.3 je dokazan.

Mnogokratnost (vrstni red) ničelne funkcije g(z)= 1//(r) se imenuje pole order funkcija /(r). če N- vrstni red pola je torej th g(z)= (r - Zo)N ip(z), in (pojdi) F 0, in kot je prikazano v prvem delu dokaza izreka 26.3, ima razširitev f(r) obliko (26.3), kjer je c_/v f 0. Nasprotno, če se f(r) razširi v vrsto (26.3) in e-z F 0, torej

t.s. N- vrstni red pola funkcije f(r). torej vrstni red zq pola funkcije/(G) je enako številu vodilnega neničelnega koeficienta glavnega dela Laurentove ekspanzije v preluknjani okolici točke zq(tj. enako takšnemu številu N, kaj s_dg f 0 in sp= 0 pri p > N).

Dokažimo naslednjo trditev, ki je priročna) za aplikacije.

Posledica 26.4. Točka zq je pol reda N fikcije/(G) če in samo če/(G) predstavljajo v obliki

kjer je h(z) analitična funkcija v okolici točke th in h(zo) f 0.

Dokaz. funkcija cp(z) = l/h(z) je analitičen v neki okolici točke r. Pogoj iz posledice 26.4 je enakovreden naslednjemu:

Zato zq - večkratnost nič n funkcije g(z). in s tem mnogoterinski pol n funkcije /(2).

II primer 26.5. Poiščite izolirane singularne točke funkcije in določi njihovo vrsto.

Deu k cija Točke, na katerih (z 2 + 1 )(z+ H) 2 = 0. Če z 2 L- 1 = 0, nato 2 = ±gče (z 4- H) 2 = 0, torej z= -3. Zato ima funkcija tri singularne točke z= r, 22 = -r, Z3 = - 3. Razmislite z:

G - pol prvega reda (uporabili smo posledico 26.4). Podobno lahko dokažemo, da je 22 = -jaz tudi pol prvega reda. Za 2h imamo:

Preidimo k obravnavi bistveno singularnih točk.

Izrek 26.6. Izolirana singularna točka zq funkcije f(z) je v bistvu singularna, če in samo če ima glavni del Laurentove ekspanzije s središčem na zq neskončno veliko različnih od. nič, koeficienti s p.

Dokaz. Izrek 26.6 sledi neposredno iz izrekov 26.2 in 26.3. Dejansko, če bistvo zq v bistvu singularen, potem glavni del Laurentove razširitve ne more biti odsoten ali vsebovati končnega števila členov (sicer točka Zq bo bodisi odstranljiv ali palica). Zato mora biti število členov v glavnem delu neskončno.

Nasprotno, če glavni del vsebuje neskončno veliko členov, potem Zq ne more biti niti odstranljiva točka niti pol. Posledično je ta točka v bistvu singularna.

V skladu z definicijo je za bistveno singularno točko značilno dejstvo, da funkcija f(2) nima niti končne niti neskončne meje za z ->zq. Popolnejšo predstavo o tem, kako nepravilno je obnašanje funkcije v okolici v bistvu singularne točke, podaja naslednji izrek.

Izrek 26.7 (Sochockijev izrek). Če je zq v bistvu singularen, potem je točka funkcije f(z), potem za poljubno kompleksno število L, vključno z A = oo, obstaja zaporedje točk z n tako, da je z n -> zo in lim f(zn) = A.

n->os

Dokaz. Najprej razmislite o primeru A = oo. V prvem delu dokaza izreka 2G.2 smo ugotovili, da če f(z) je omejena v neki preluknjani okolici točke r0, potem vsi koeficienti c, n = - 1, - 2,... glavnega dela so enake nič (in posledično je singularnost v th odstranljiva). Ker je po predpostavki r0 v bistvu singularna točka, je funkcija f(r) neomejena v kateri koli preluknjani okolici točke r0. Vzemimo neko ozko okolico 0 Z tako, da f(zi) > 1 (če |/(r)| z - zo R/2 obstaja točka z-2 , kjer je |/(dd)| > 2 itd.: v preluknjani soseski O 71. Očitno je, da je rn -e go in lim /(r«) = oo. Tako v primeru A = oo velja izrek 26.7

dokazano.

Naj zdaj A f oo. Najprej predpostavimo, da obstaja preluknjana soseska 0

= -yy---- bo v tej preluknjani soseski analitičen in posledično

/(G) - A

posledično je r izolirana singularna točka funkcije Φ(r). Pokažimo. da je r0 v bistvu singularna točka Φ(r). Naj bo narobe. Potem obstaja limit lim Φ(r), bodisi končen bodisi neskončen. Ker

/(r) = A + , potem obstaja tudi Hsh /(r), kar je v nasprotju s pogojem

F(g) ~ :-*z 0

pogled na izrek. Tako je r0 v bistvu singularna točka funkcije Φ(r). Glede na zgoraj dokazano obstaja zaporedje točk r n tako, da je r n o in lim Φ(r n) = oo. Od tod

Zahtevano trditev smo dokazali ob predpostavki, da je f(r) F A v neki preluknjani okolici točke r. Predpostavimo zdaj, da to ni res, tj. v kateri koli poljubno majhni preluknjani okolici točke th je taka točka G", da je f(r") = A. Potem za poljubno p v preluknjani okolici 0 f(z u) = L. Zahtevana trditev torej drži p-juo

v vseh primerih in izrek 26.7 je dokazan.

V skladu s (Sokhotskyjevim) izrekom 26.7 ima funkcija f(r) v kateri koli (poljubno majhni) preluknjani soseščini v bistvu singularne točke vrednosti, ki so poljubno blizu kateremu koli številu v razširjeni kompleksni ravnini C.

Za preučevanje izoliranih singularnih točk so pogosto uporabne znane Taylorjeve razširitve osnovnih elementarnih funkcij.

PRIMER 2G.8. Določite vrsto singularne točke zq = 0 za funkcijo

Rešeno in e. Števec in imenovalec razširimo v Taylorjev niz po potencah r. Zamenjava v (22.11) 3 z namesto r in odštejemo 1, dobimo

Z uporabo (22.12) dobimo razširitev imenovalca:

Nizi v teh razširitvah konvergirajo v celotni kompleksni ravnini €. Imamo

in /2(2) sta analogna v okolici točke zo = 0 (in celo v celi ravnini) in /2(20) F 0, torej h(z) je tudi analitična v neki okolici točke gF 0. V skladu s posledico 26.4 je točka Zo = 0 je pol reda N = 4.

II primer 26.9. Poiščite singularne točke funkcije f(z)= sin j - in določi njihovo vrsto.

P e in e in e. Funkcija ima eno samo končno singularno točko zq = 1. V drugih točkah iz C je funkcija w =--- analitični; torej funkcija greha w bo analitično.

Zamenjava v razširitvi sinusa (22.12) - namesto r dobimo

Dobili smo ekspanzijo funkcije sin v Laurentovem nizu v preluknjani okolici točke 20 = 1. Ker nastala ekspanzija vsebuje neskončno veliko členov z negativnimi potencami (r - 1), potem zq = 1 je bistvena singularna točka (v tem primeru je Laurentova ekspanzija sestavljena samo iz glavnega dela, pravilni del pa manjka).

Upoštevajte, da je bilo tudi v tem primeru mogoče ugotoviti naravo singularnosti neposredno iz definicije, ne da bi se zatekli k razširitvi serije. Dejansko obstajata zaporedja (r") in (2"), ki konvergirata k zo= 1, in tako, da f(z" n)= 1, /(2") = 0 (taka zaporedja določite sami). Torej, f(z) nima omejitev, kdaj z -> 1 in s tem bistvo zq - 1 je v bistvu ednina.

Predstavimo koncept Laurentove ekspanzije funkcije v okolici točke Zq = 00 in upoštevajte povezavo med ekspanzijo in naravo singularnosti na tej točki. Upoštevajte, da se definicije izolirane singularne točke in njene vrste (odstranljiva, polna ali v bistvu singularna) prenesejo na primer zq = oc nespremenjeno. Toda izreki 26.2. 26.3 in 26.6, povezana z naravo Laurentovih razširitev, je treba spremeniti. Bistvo je, da člani c n (z - 2o) str. p= -1,-2,..., glavni del, ki določa "nepravilnost" funkcije blizu končne točke Zq, ko 2 teži k oo, se bodo obnašali »pravilno« (težijo k 0). Nasprotno, člani rednega dela z p= 1,2,... bo težilo k oo; določajo naravo singularnosti v Zq = oo. Zato bodo glavni del širitve v soseščini oo termini s pozitivnimi močmi P, in pravilno - z negativnim.

Predstavimo novo spremenljivko w = 12. funkcija tv= 1/2, razširjen tako, da je u(oo) = 0, ena proti ena in konformno preslika sosesko z > R točke zq = 00 v okolici |w| wq = 0. Če je funkcija f(z) analitika v preluknjani soseski R z Zq = oc, potem funkcija G(w) = f(l/w) bo analitično v rumeni soseščini 0 wo = 0. Ker bo za 2 -> oo obstajalo w-> 0, torej

Zato G(w) ima na točki wq = 0 je singularnost iste vrste kot f(z) na točki Zq = 00. Razširimo funkcijo G(w) v Laurentovo vrsto v preluknjani okolici točke wo = 0:

Vsota na desni strani (26.5) predstavlja pravilen oziroma glavni del razširitve. Pojdimo k spremenljivki z, nadomeščanje w = 1/z:

označevanje p\u003d -A *, 6 * \u003d 6_ " \u003d s p in to opaziti G(l/z) = f(z), dobimo

Razpad (2G.G) se imenuje Laurentova ekspanzija funkcije f(z) v preluknjani okolici točke zq= oo. Prva vsota v (2G.6) se imenuje desni del, druga vsota pa je glavni del ta razgradnja. Ker te vsote ustrezajo pravilnim in glavnim delom razširitve (26.5), razširitev (26.6) zadošča analogom izrekov 26.2, 26.3 in 26.6. Tako je naslednji izrek analog izreka 26.2.

Izrek 26.10. Izolirana singularna točkaZq - os (funkcije/(G) je odstranljiv, če in samo če ima Laurentov razteg v preluknjani okolici te točke obliko

t.s. je sestavljen samo iz pravilnega dela.

Postavimo /(oo) = co. Funkcija, definirana z vrsto (26.7), ki konvergira v soseščini z > R točke 2o \u003d oc, imenovane analitično v točki z o = oo. (Upoštevajte, da je ta definicija enakovredna analitičnosti funkcije G (š) na točki wo = 0.)

Primer 26.11. Raziščite singularno točko zq = oo funkcije

Ker je meja končna, torej zo = oo je odstranljiva singularna točka funkcije f(r). Če postavimo /(oo) = lim J(z)= 0, torej f(z) bo

tik na točki Zo= os. Pokažimo, kako najdemo ustrezno razširitev (26.7). Pojdimo k spremenljivki w = 1 fz. Nadomeščanje z= 1 /?e, dobimo

(zadnja enakost velja v preluknjani okolici točke ww = 0, vendar bomo definicijo razširili (7(0) = 0). Dobljena funkcija ima singularne točke w =±i, w =-1/3, in na točki Wq = 0 je analitično. Funkcija razširitve G(w) po stopinjah w(kot je bilo storjeno v primeru 25.7) in zamenjavo v dobljeni potenčni niz w = 1/z lahko dobimo razširitev (26.7) funkcije f(z).

Izrek 26.3 za primer zo= oo bo prepisan v naslednji obliki.

Izrek 26.12. Izolirana singularna točka pojdi = os funkcija f(z) je pol, če in samo če je glavni del Laurentove ekspanzije (26.6) ima samo končno število neničelnih koeficientov z":

Tukaj je vrsta pravilni del, polinom v oklepaju pa je glavni del razširitve. Večkratnost pola v oc je definirana kot večkratnost pola wq = 0 funkcij G(z). Preprosto je videti, da množica pola sovpada s številom n v (26,8).

Q p | (i 2 + 1) (z + 3) 2

Naloga. Pokažite, da funkcija f(z) =-- -- ima v

točka zo = oo naročilo drogov 3.

Izrek 26.6 o bistveni singularni točki je prepisan za ta primer zo= os skoraj dobesedno in se na njem ne zadržujemo podrobneje.