Séries de Fourier. Determinando os coeficientes de uma série usando as fórmulas de Fourier Expandir uma função periódica em uma série de Fourier

Série de Fourier de funções periódicas de período 2π.

A série de Fourier permite estudar funções periódicas decompondo-as em componentes. Correntes e tensões alternadas, deslocamentos, velocidade e aceleração de mecanismos de manivela e ondas acústicas são exemplos práticos típicos da aplicação de funções periódicas em cálculos de engenharia.

A expansão da série de Fourier é baseada na suposição de que todas as funções de importância prática no intervalo -π ≤ x ≤ π podem ser expressas como séries trigonométricas convergentes (uma série é considerada convergente se a sequência de somas parciais composta por seus membros converge) :

Notação padrão (=usual) através da soma de senx e cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 senx+b 2 sen2x+b 3 sen3x+...,

onde a o , a 1 ,a 2 ,...,b 1 ,b 2 ,.. são constantes reais, ou seja,

Onde, para o intervalo de -π a π, os coeficientes da série de Fourier são calculados pelas fórmulas:

Os coeficientes a o , a n e b n são chamados Coeficientes de Fourier, e se eles puderem ser encontrados, então a série (1) é chamada perto de Fourier, correspondente à função f(x). Para a série (1), o termo (a 1 cosx+b 1 senx) é chamado de primeiro ou gaita principal,

Outra maneira de escrever uma série é usar a relação acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Onde a o é uma constante, c 1 \u003d (a 1 2 +b 1 2) 1/2, c n \u003d (a n 2 +b n 2) 1/2 são as amplitudes dos vários componentes e é igual a a n \ u003d arctg a n /b n.

Para a série (1), o termo (a 1 cosx + b 1 senx) ou c 1 sen (x + α 1) é chamado de primeiro ou gaita principal,(a 2 cos2x+b 2 sin2x) ou c 2 sin(2x+α 2) é chamado segundo harmônico e assim por diante.

Para representar com precisão um sinal complexo, geralmente é necessário um número infinito de termos. Entretanto, em muitos problemas práticos é suficiente considerar apenas os primeiros termos.

Série de Fourier de funções não periódicas de período 2π.

Decomposição de funções não periódicas.

Se a função f(x) for não periódica, então ela não pode ser expandida em uma série de Fourier para todos os valores de x. No entanto, é possível definir uma série de Fourier representando uma função em qualquer faixa de largura 2π.

Dada uma função não periódica, pode-se compor uma nova função escolhendo valores de f(x) dentro de um determinado intervalo e repetindo-os fora desse intervalo em intervalos de 2π. Como a nova função é periódica com período de 2π, ela pode ser expandida em uma série de Fourier para todos os valores de x. Por exemplo, a função f(x)=x não é periódica. No entanto, se for necessário expandi-lo em uma série de Fourier no intervalo de 0 a 2π, então uma função periódica com período de 2π é construída fora desse intervalo (conforme mostrado na figura abaixo).

Para funções não periódicas como f(x)=x, a soma da série de Fourier é igual ao valor de f(x) em todos os pontos do intervalo dado, mas não é igual a f(x) para pontos fora da faixa. Para encontrar a série de Fourier de uma função não periódica no intervalo 2π, usa-se a mesma fórmula dos coeficientes de Fourier.

Funções pares e ímpares.

Eles dizem que a função y=f(x) até se f(-x)=f(x) para todos os valores de x. Gráficos de funções pares são sempre simétricos em relação ao eixo y (ou seja, são espelhados). Dois exemplos de funções pares: y=x 2 e y=cosx.

Eles dizem que a função y=f(x) chance, se f(-x)=-f(x) para todos os valores de x. Gráficos de funções ímpares são sempre simétricos em relação à origem.

Muitas funções não são nem pares nem ímpares.

Expansão em série de Fourier em cossenos.

A série de Fourier de uma função periódica par f(x) com período 2π contém apenas termos de cosseno (ou seja, não contém termos de seno) e pode incluir um termo constante. Por isso,

onde são os coeficientes da série de Fourier,

A série de Fourier de uma função periódica ímpar f(x) com período 2π contém apenas termos com senos (ou seja, não contém termos com cossenos).

Por isso,

onde são os coeficientes da série de Fourier,

Série de Fourier em um semiciclo.

Se uma função é definida para um intervalo, digamos 0 a π, e não apenas 0 a 2π, ela pode ser expandida em uma série apenas em termos de senos ou apenas em termos de cossenos. A série de Fourier resultante é chamada perto de Fourier em meio ciclo.

Se você deseja obter uma decomposição Fourier em um meio ciclo em cossenos funções f(x) no intervalo de 0 a π, então é necessário compor uma função periódica par. Na fig. abaixo está a função f(x)=x construída no intervalo de x=0 a x=π. Como a função par é simétrica em relação ao eixo f(x), desenhamos a linha AB, conforme mostrado na Fig. abaixo. Se assumirmos que fora do intervalo considerado, a forma triangular resultante é periódica com um período de 2π, então o gráfico final tem a forma, display. na fig. abaixo. Como é necessário obter a expansão de Fourier em cossenos, como antes, calculamos os coeficientes de Fourier a o e an

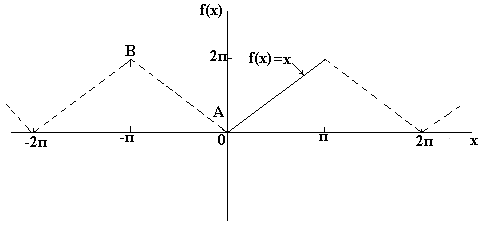
Se você precisa obter Expansão de Fourier de meio ciclo senoidal função f(x) no intervalo de 0 a π, então é necessário compor uma função periódica ímpar. Na fig. abaixo está a função f(x)=x construída no intervalo de x=0 a x=π. Como a função ímpar é simétrica em relação à origem, construímos a linha CD, conforme mostrado na Fig. Se assumirmos que fora do intervalo considerado, o sinal dente de serra recebido é periódico com período de 2π, então o gráfico final tem a forma mostrada na Fig. Como é necessário obter a expansão de Fourier em um meio ciclo em termos de senos, como antes, calculamos o coeficiente de Fourier. b

Série de Fourier para um intervalo arbitrário.

Expansão de uma função periódica com período L.

A função periódica f(x) se repete à medida que x aumenta em L, ou seja, f(x+L)=f(x). A transição das funções de período 2π consideradas anteriormente para funções de período L é bastante simples, pois pode ser feita por meio de uma mudança de variável.

Para encontrar a série de Fourier da função f(x) no intervalo -L/2≤x≤L/2, introduzimos uma nova variável u de modo que a função f(x) tenha um período de 2π em relação a u. Se u=2πx/L, então x=-L/2 para u=-π ex=L/2 para u=π. Seja também f(x)=f(Lu/2π)=F(u). A série de Fourier F(u) tem a forma

(Os limites de integração podem ser substituídos por qualquer intervalo de comprimento L, por exemplo, de 0 a L)

Série de Fourier em semiciclo para funções dadas no intervalo L≠2π.

Para a substituição u=πx/L, o intervalo de x=0 a x=L corresponde ao intervalo de u=0 a u=π. Portanto, a função pode ser expandida em uma série apenas em termos de cossenos ou apenas em termos de senos, ou seja, V Série de Fourier em um meio ciclo.

A expansão em cossenos no intervalo de 0 a L tem a forma

2. Determinação dos coeficientes da série pelas fórmulas de Fourier.

Seja uma função periódica ƒ(x) de período 2π tal que seja representada por uma série trigonométrica convergindo para uma dada função no intervalo (-π, π), ou seja, é a soma desta série:

Suponha que a integral da função do lado esquerdo dessa igualdade seja igual à soma das integrais dos termos dessa série. Isso será verdade se assumirmos que a série de números composta pelos coeficientes da série trigonométrica dada converge absolutamente, ou seja, a série de números positivos converge

A série (1) é majoritária e pode ser integrada termo a termo no intervalo (-π, π). Integramos ambas as partes da igualdade (2):

Calculamos separadamente cada integral que ocorre no lado direito:

,

,

Por isso, , onde

. (4)

Estimação dos coeficientes de Fourier. (Bugrov)

Teorema 1. Deixe uma função ƒ(x) de período 2π ter uma derivada contínua ƒ (s) (x) de ordem s que satisfaça a desigualdade em todo o eixo real:

│ ƒ (s) (x)│≤ M s ; (5)

então os coeficientes de Fourier da função ƒ satisfazem a desigualdade

Prova. Integrando por partes e levando em conta que

ƒ(-π) = ƒ(π), temos

Integrando o lado direito de (7) sequencialmente, levando em consideração que as derivadas ƒ ΄ , …, ƒ (s-1) são contínuas e assumem os mesmos valores nos pontos t = -π e t = π, também como estimativa (5), obtemos a primeira estimativa (6).

A segunda estimativa (6) é obtida de maneira similar.

Teorema 2. Os coeficientes de Fourier ƒ(x) satisfazem a desigualdade

(8)

Prova. Nós temos

(9)

Introduzindo neste caso uma mudança de variável e tendo em conta que ƒ(x) é uma função periódica, obtemos

Somando (9) e (10), obtemos

Realizamos a prova para b k de maneira similar.

Consequência. Se a função ƒ(x) é contínua, então seus coeficientes de Fourier tendem a zero: a k → 0, b k → 0, k → ∞.

Espaço de funções com produto escalar.

Uma função ƒ(x) é chamada de contínua por partes em um segmento se ela for contínua nesse segmento, exceto talvez por um número finito de pontos onde possui descontinuidades do primeiro tipo. Esses pontos podem ser adicionados e multiplicados por números reais e, como resultado, funções contínuas por partes em um segmento podem ser obtidas.

O produto escalar de duas partes contínuas em (a< b) функций ƒ и φ будем называть интеграл

(11)

Obviamente, para quaisquer funções contínuas por partes ƒ , φ , ψ valem as seguintes propriedades:

1) (ƒ , φ) =(φ, ƒ);

2) (ƒ , ƒ) e a igualdade (ƒ , ƒ) = 0 implica que ƒ(x) =0 em , excluindo, talvez, um número finito de pontos x;

3) (α ƒ + β φ , ψ) = α (ƒ , ψ) + β (φ , ψ),

onde α, β são números reais arbitrários.

O conjunto de todas as funções contínuas por partes definidas no intervalo , para o qual o produto escalar é introduzido de acordo com a fórmula (11), denotaremos, e espaço de chamada

Observação 1.

Em matemática, um espaço = (a, b) é um conjunto de funções ƒ(x) que são integráveis ​​no sentido de Lebesgue em conjunto com seus quadrados, para o qual o produto escalar é introduzido pela fórmula (11). O espaço em questão faz parte de . O espaço tem muitas das propriedades do espaço, mas não todas.

As propriedades 1), 2), 3) implicam a importante desigualdade de Bunyakovskii | (ƒ , φ) | ≤ (ƒ , ƒ) ½ (φ , φ) ½ , que na linguagem de integrais fica assim:

Valor

é chamada de norma da função f.

A norma tem as seguintes propriedades:

1) || f || ≥ 0, enquanto a igualdade só pode ser para a função zero f = 0, ou seja, a função igual a zero, exceto, talvez, para um número finito de pontos;

2) || ƒ + φ || ≤ || ƒ(x) || || φ ||;

3) || αƒ || = | α | · || ƒ ||,

onde α é um número real.

A segunda propriedade na linguagem de integrais se parece com isso:

e é chamada de desigualdade de Minkowski.

Diz-se que uma sequência de funções ( f n ), pertence a , converge para uma função pertence no sentido do quadrado médio em (ou então na norma ), se

Note que se a sequência de funções ƒ n (x) converge uniformemente para a função ƒ(x) no segmento , então para n suficientemente grande a diferença ƒ(x) - ƒ n (x) em valor absoluto deve ser pequena para todos x do segmento.

Se ƒ n (x) tende a ƒ (x) no sentido quadrático médio no segmento , então a diferença indicada pode não ser pequena para n grande em qualquer lugar em . Em alguns lugares do segmento, essa diferença pode ser grande, mas é importante apenas que a integral de seu quadrado sobre o segmento seja pequena para n grande.

Exemplo. Considere uma dada função linear contínua por partes ƒ n (x) (n = 1, 2,…) mostrada na figura, e

(Bugrov, p. 281, fig. 120)

Para qualquer n natural

e, consequentemente, esta sequência de funções, embora converja para zero quando n → ∞, não é uniforme. Enquanto isso

ou seja, a sequência de funções (f n (x)) tende a zero no sentido do quadrado médio em .

A partir dos elementos de alguma sequência de funções ƒ 1 , ƒ 2 , ƒ 3 ,… (pertencente a ) construímos uma série

ƒ 1 + ƒ 2 + ƒ 3 +… (12)

A soma de seus primeiros n membros

σ n = ƒ 1 + ƒ 2 + … + ƒ n

existe uma função que pertence a . Se acontecer de lá existir uma função ƒ tal que

|| ƒ-σ n || → 0 (n → ∞),

então dizemos que a série (12) converge para a função ƒ no sentido do quadrado médio e escrevemos

ƒ = ƒ 1 + ƒ 2 + ƒ 3 +…

Observação 2.

Pode-se considerar o espaço = (a, b) de funções de valores complexos ƒ(x) = ƒ 1 (x) + iƒ 2 (x), onde ƒ 1 (x) e ƒ 2 (x) são funções reais contínuas por partes . Neste espaço, as funções são multiplicadas por números complexos e o produto escalar das funções ƒ(x) = ƒ 1 (x) + iƒ 2 (x) e φ(x) = φ 1 (x) + i φ 2 (x) é definido da seguinte forma:

e a norma ƒ é definida como o valor

Expansão em série de Fourier de funções pares e ímpares expansão de uma função dada em um segmento em uma série em termos de senos ou cossenos Série de Fourier para uma função com um período arbitrário Representação complexa da série de Fourier Série de Fourier em geral sistemas ortogonais de funções Série de Fourier em um sistema ortogonal Propriedade mínima dos coeficientes de Fourier Desigualdade de Bessel Igualdade Parseval Sistemas fechados Completude e fechamento de sistemas

Expansão em série de Fourier de funções pares e ímpares A função f(x), definida no segmento \-1, onde I > 0, é chamada mesmo que o gráfico da função par seja simétrico em relação ao eixo y. A função f(x) definida no segmento J, onde I > 0, é chamada ímpar se o gráfico da função ímpar for simétrico em relação à origem. Exemplo. a) A função é par no segmento |-jt, jt), pois para todo x e b) A função é ímpar, pois a expansão em série de Fourier de funções pares e ímpares é a expansão de uma função dada no segmento em uma série de senos ou cossenos Série de Fourier para uma função com um período arbitrário Notação complexa da série de Fourier Série de Fourier em sistemas ortogonais gerais de funções Série de Fourier em um sistema ortogonal Propriedade mínima dos coeficientes de Fourier Desigualdade de Bessel Igualdade de Parseval Sistemas fechados Completude e fechamento de sistemas c) Função f(x)=x2-x, onde não pertence nem a funções pares nem a funções ímpares, desde que a função f(x) satisfazendo as condições do Teorema 1 seja par no segmento x|. Então, para todos, ou seja, /(g) cos nx é uma função par e f(x)sinnx é ímpar. Portanto, os coeficientes de Fourier de uma função par /(x) serão iguais Portanto, a série de Fourier de uma função par tem a forma f(x) sen nx é uma função par. Portanto, teremos Assim, a série de Fourier de uma função ímpar tem a forma Aplicando a integração por partes duas vezes, obtemos que Assim, a série de Fourier desta função se parece com isto: ou, na forma expandida, Esta igualdade é válida para qualquer x €, já que nos pontos x = ±ir a soma dos série coincide com os valores da função f(x ) = x2, pois os gráficos da função f(x) = x e as somas das séries resultantes são dadas na fig. Comente. Esta série de Fourier permite encontrar a soma de uma das séries numéricas convergentes, ou seja, para x \u003d 0, obtemos que A função /(x) satisfaz as condições do Teorema 1, portanto pode ser expandida em uma série de Fourier, que, pela estranheza dessa função, terá a forma Integrando por partes, encontramos os coeficientes de Fourier Portanto, o Fourier série desta função tem a forma Esta igualdade vale para todos os pontos x  x - ±tg a soma da série de Fourier não coincide com os valores da função / (x) = x, pois é igual a Fora do segmento [- *, n-] a soma da série é uma continuação periódica da função / (x) \u003d x; seu gráfico é mostrado na Fig. 6. § 6. Expansão de uma função dada em um intervalo em uma série em termos de senos ou cossenos. Os valores desta função no intervalo 0| pode ser definido de várias maneiras. Por exemplo, é possível definir a função / no segmento mc] de forma que /. Neste caso diz-se que) "estende-se ao segmento 0] de forma uniforme"; sua série de Fourier conterá apenas cossenos. Se, no entanto, a função /(x) for definida no segmento [-x, mc] de modo que /(, então uma função ímpar seja obtida, e então dizemos que / "é estendida ao segmento [-*, 0 ] de maneira ímpar"; neste caso, a série de Fourier conterá apenas senos. senos e cossenos.Exemplo 1. Expandir a função em uma série de Fourier: a) por cossenos; b) ao longo dos senos. M Esta função, com suas extensões pares e ímpares para o segmento |-x, 0) será limitada e monotônica por partes. a) Continuamos / (z) no segmento 0) a) Continuamos j \ x) no segmento (-m, 0 | de maneira uniforme (Fig. 7), então sua série de Fourier i terá a forma P \u003d 1 onde os coeficientes de Fourier são iguais, respectivamente para Portanto, b) Vamos continuar /(z) no segmento [-x,0] de forma ímpar (Fig. 8). Então sua série de Fourier §7. Série de Fourier para uma função com período arbitrário Deixe a função fix) ser periódica com um período de 21,1 ^ 0. Para expandi-la em uma série de Fourier no intervalo onde I > 0, fazemos uma mudança de variável definindo x = jt . Então a função F(t) = / ^tj será uma função periódica do argumento t com um período e pode ser expandida em um segmento em uma série de Fourier Voltando à variável x, ou seja, estabelecendo, obtemos , permanecemos em vigor também para funções periódicas com um período arbitrário 21. Em particular, o critério suficiente para a expansão de uma função em uma série de Fourier também permanece válido. Exemplo 1. Expandir em uma série de Fourier uma função periódica com um período de 21, dado no segmento [-/,/] pela fórmula (Fig. 9). Como essa função é par, sua série de Fourier tem a forma Substituindo os valores encontrados dos coeficientes de Fourier na série de Fourier, obtemos Notamos uma propriedade importante das funções periódicas. Teorema 5. Se uma função tem um período T e é integrável, então para qualquer número a a igualdade m vale. ou seja, a integral em um segmento cujo comprimento é igual ao período T tem o mesmo valor independentemente da posição deste segmento no eixo real. De fato, Fazemos uma mudança de variável na segunda integral, assumindo Isso dá e, portanto, geometricamente, essa propriedade significa que, no caso da área sombreada na Fig. 10 áreas são iguais entre si. Em particular, para uma função f(x) com um período, obtemos na expansão em série de Fourier de funções pares e ímpares a expansão de uma função dada em um segmento em uma série em termos de senos ou cossenos Série de Fourier para uma função com um período arbitrário Representação complexa da série de Fourier Série de Fourier em geral funções de sistemas ortogonais Série de Fourier em um sistema ortogonal Propriedade mínima dos coeficientes de Fourier Desigualdade de Bessel Igualdade de Parseval Sistemas fechados Completude e fechamento de sistemas que os coeficientes de Fourier de uma função periódica f(x) com um período de 21 pode ser calculado usando as fórmulas em que a é um número real arbitrário (observe que as funções cos - e sin têm um período de 2/). Exemplo 3. Expanda em uma série de Fourier uma função dada em um intervalo com um período de 2x (Fig. 11). 4 Encontre os coeficientes de Fourier desta função. Colocando nas fórmulas descobrimos que para Portanto, a série de Fourier ficará assim: No ponto x = jt (ponto de descontinuidade do primeiro tipo) temos §8. Notação complexa da série de Fourier Nesta seção, alguns elementos da análise complexa são usados ​​(ver Capítulo XXX, onde todas as operações aqui realizadas com expressões complexas são estritamente justificadas). Deixe a função f(x) satisfazer condições suficientes para expansão em uma série de Fourier. Então no segmento x] pode ser representado por uma série da forma Usando as fórmulas de Euler Substituindo essas expressões na série (1) em vez de cos nx e sen xy teremos Introduzimos a seguinte notação Então a série (2) assume a forma Assim, a série de Fourier (1) é apresentada na forma complexa (3). Vamos encontrar expressões para os coeficientes em termos de integrais. Da mesma forma, encontramos Finalmente, as fórmulas para с„, с_п e с podem ser escritas da seguinte forma: . . Os coeficientes cn são chamados de coeficientes de Fourier complexos da função Para uma função periódica com um período), a forma complexa da série de Fourier assume os valores de forma w se existirem limites Exemplo. Expandir a função de período em uma série de Fourier complexa Esta função satisfaz condições suficientes para a expansão em uma série de Fourier. Vamos Encontre os coeficientes de Fourier complexos desta função. Temos para ímpar para par n, ou, resumindo. Substituindo os valores), finalmente obtemos Note que esta série também pode ser escrita da seguinte forma: Série de Fourier em sistemas ortogonais gerais de funções 9.1. Sistemas ortogonais de funções Denotam pelo conjunto de todas as funções (reais) que são quadradas e integráveis ​​no intervalo [a, 6], ou seja, aquelas para as quais existe uma integral. Em particular, todas as funções f(x) que são contínuas no intervalo [a , 6], pertencem a 6], e os valores de suas integrais de Lebesgue coincidem com os valores das integrais de Riemann. Definição. O sistema de funções, onde, é dito ortogonal no intervalo [a, b\, se a Condição (1) assume, em particular, que nenhuma das funções é identicamente igual a zero. A integral é entendida no sentido de Lebesgue. e chamamos a quantidade de norma de uma função.Se em um sistema ortogonal para qualquer n temos, então o sistema de funções é chamado ortonormal. Se o sistema (y>n(x)) for ortogonal, então o sistema Exemplo 1. Um sistema trigonométrico é ortogonal em um segmento. O sistema de funções é um sistema de funções ortonormais, Exemplo 2. O sistema de cossenos e o sistema de senos são ortonormais. Vamos introduzir a notação de que são ortogonais no segmento (0, f|, mas não ortonormais (para I ↦ 2). Como suas normas são COS, as funções formam um sistema ortonormal de funções em um segmento. Vamos mostrar, por exemplo, que os polinômios de Legendre são ortogonais. Seja m > n. Nesse caso, integrando n vezes por partes, encontramos, pois para a função t/m = (z2 - I)m, todas as derivadas até a ordem m - Eu inclusive desapareço nas extremidades do intervalo [-1,1). Definição. O sistema de funções (pn(x)) é chamado ortogonal no intervalo (a, b) pela saliência p(x) se: 1) existem integrais para todo n = 1,2,... Aqui assume-se que a função de peso p(x) é definida e positiva em todo o intervalo (a, b), com a possível exceção de um número finito de pontos onde p(x) pode desaparecer. Depois de realizar a diferenciação na fórmula (3), encontramos. Pode-se mostrar que os polinômios de Chebyshev-Hermite são ortogonais no intervalo Exemplo 4. O sistema de funções de Bessel (jL(pix)^ é ortogonal no intervalo de zeros do sistema de funções de Bessel Seja um sistema ortogonal de funções no intervalo (a, 6) e deixe a série (cj = const) convergir neste intervalo para a função f(x): Em virtude da ortogonalidade do sistema, obtemos que Esta operação tem, em geral, um caráter puramente formal. Porém, em alguns casos, por exemplo, quando a série (4) converge uniformemente, todas as funções são contínuas e o intervalo (a, 6) é finito, essa operação é legal. Mas é a interpretação formal que é importante para nós agora. Então, digamos que uma função é dada. Formamos os números c * de acordo com a fórmula (5) e escrevemos A série do lado direito é chamada de série de Fourier da função f (x) em relação ao sistema (^n (n)) - Os números Cn são chamados de coeficientes de Fourier da função f(x) neste sistema. O sinal ~ na fórmula (6) significa apenas que os números Cn estão relacionados à função f(x) pela fórmula (5) (neste caso, não se assume que a série à direita converge, muito menos converge para a função f(x)). Portanto, surge naturalmente a pergunta: quais são as propriedades dessa série? Em que sentido ela "representa" a função f(x)? 9.3. Definição de Convergência Média. Uma sequência converge para um elemento ] em média se a norma estiver no espaço Teorema 6. Se uma sequência ) converge uniformemente, então ela também converge em média. M Deixe a sequência ()) convergir uniformemente no segmento [a, b] para a função f(x). Isso significa que para qualquer, para todo n suficientemente grande, temos Daí, do qual segue nossa afirmação. A recíproca não é verdadeira: a sequência () pode convergir em média para /(x), mas não ser uniformemente convergente. Exemplo. Consideremos a sequência nx É fácil ver que Mas essa convergência não é uniforme: existe e, por exemplo, tal que não importa quão grande seja n, no segmento Série de Fourier para uma função com período arbitrário Representação complexa de a série de Fourier Série de Fourier em sistemas ortogonais gerais de funções Série de Fourier em um sistema ortogonal Propriedade mínima dos coeficientes de Fourier Desigualdade de Bessel Igualdade de Parseval Sistemas fechados Completude e fechamento de sistemas e let ) no sistema ortonormal b Considere uma combinação linear onde n ^ 1 é um inteiro fixo e encontre os valores das constantes para as quais a integral assume seu valor mínimo. Vamos escrevê-lo com mais detalhes Integrando termo a termo, devido à ortonormalidade do sistema, obtemos Os dois primeiros termos do lado direito da igualdade (7) são independentes e o terceiro termo é não negativo. Portanto, a integral (*) assume um valor mínimo em ak = sk. A integral é chamada de aproximação da raiz quadrada média da função f(x) como uma combinação linear de Tn(x). Assim, a aproximação da raiz quadrada média da função /\ assume um valor mínimo quando. quando Tn(x) é a 71ª soma parcial da série de Fourier da função /(x) no sistema (. Definindo ak = ck, de (7) obtemos a igualdade (9) é chamada de identidade de Bessel. lado é não negativo, então a partir dele segue a desigualdade de Bessel Como i é arbitrário aqui, a desigualdade de Bessel pode ser representada de forma reforçada, ou seja, para qualquer função /, a série de coeficientes de Fourier quadrados desta função em um sistema ortonormal ) converge . Como o sistema é ortonormal no segmento [-x, r], então a desigualdade (10) traduzida na notação usual da série trigonométrica de Fourier fornece a relação válida para qualquer função f(x) com um quadrado integrável. Se f2(x) é integrável, então, em virtude da condição necessária para a convergência da série do lado esquerdo da desigualdade (11), obtemos isso. Igualdade de Parseval Para alguns sistemas (^n(x)) o sinal de desigualdade na fórmula (10) pode ser substituído (para todas as funções f(x) 6 x) por um sinal de igual. A igualdade resultante é chamada de igualdade de Parseval-Steklov (condição de completude). A identidade de Bessel (9) nos permite escrever a condição (12) de forma equivalente pela norma espacial 6]. Definição. Um sistema ortonormal ( é chamado completo em b2[ay b] se qualquer função pode ser aproximada com alguma precisão na média por uma combinação linear da forma com um número suficientemente grande de termos, ou seja, se para qualquer função f(x) ∈ b2[a, b\ e para qualquer e > 0 existe um número natural nq e números a\, a2y..., tais que Não. Teorema 7. Se o sistema ) é completo no espaço por ortonormalização, a série de Fourier de qualquer função / neste sistema converge para f( x) na média, ou seja, de acordo com a norma Pode-se mostrar que o sistema trigonométrico é completo no espaço. Isso implica a afirmação. Teorema 8. Se uma função /0 sua série trigonométrica de Fourier converge para ela na média. 9.5. sistemas fechados. Integralidade e fechamento de sistemas Definição. Um sistema ortonormal de funções \, é dito fechado se no espaço Li\a, b) não existe nenhuma função diferente de zero ortogonal a todas as funções. No espaço L2\a, b\ os conceitos de completude e fechamento de sistemas ortonormais coincidir. Exercícios 1. Expandir a função na série de Fourier no intervalo (-i-, x) 2. Expandir a função na série de Fourier no intervalo (-r, r) 3. Expandir a função na série de Fourier no intervalo (-r, r) 4. Expanda em uma série de Fourier na função de intervalo (-jt, r) 5. Expanda em uma série de Fourier no intervalo (-r, r) a função f(x) = x + x. 6. Expanda em uma série de Fourier no intervalo (-jt, r) a função n 7. Expanda em uma série de Fourier no intervalo (-r, x) a função / (x) \u003d sin2 x. 8. Expandir em série de Fourier no intervalo (-m, jt) a função f(x) = y 9. Expandir em série de Fourier no intervalo (-mm, -k) a função f(x) = | sinx|. 10. Expanda em uma série de Fourier no intervalo (-x-, r) a função f(x) = g. 11. Expanda em uma série de Fourier no intervalo (-r, r) a função f (x) \u003d sin §. 12. Expandir em série de Fourier a função f(x) = n -2x, dada no intervalo (0, x), continuando-a no intervalo (-x, 0): a) de forma par; b) de forma estranha. 13. Expanda em uma série de Fourier em termos de senos a função / (x) \u003d x2, dada no intervalo (0, x). 14. Expanda em uma série de Fourier a função /(x) \u003d 3-x, dada no intervalo (-2,2). 15. Expanda em uma série de Fourier a função f(x) \u003d |x |, dada no intervalo (-1,1). 16. Expanda em uma série de Fourier em termos de senos a função f (x) \u003d 2x, especificada no intervalo (0,1).

transcrição

1 MINISTÉRIO DA EDUCAÇÃO E CIÊNCIA DA FEDERAÇÃO RUSSA UNIVERSIDADE ESTADUAL DE NOVOSIBIRSK FACULDADE DE FÍSICA R. K. Belkheeva SÉRIE FOURIER EM EXEMPLOS E TAREFAS Tutorial Novosibirsk 211

2 UDC BBK V161 B44 B44 Série Belkheeva R. K. Fourier em exemplos e problemas: Textbook / Novosib. estado un-t. Novosibirsk, s. ISBN O tutorial fornece informações básicas sobre a série Fourier, fornece exemplos para cada tópico estudado. Um exemplo de aplicação do método de Fourier para resolver o problema de vibrações transversais de uma corda é analisado em detalhes. Material ilustrativo é fornecido. Existem tarefas para solução independente. Destina-se a alunos e professores da Faculdade de Física da Universidade Estadual de Novosibirsk. Publicado de acordo com a decisão da Comissão Metodológica da Faculdade de Física da NSU. Revisor Dr. phys.-math. Ciências. V. A. Aleksandrov ISBN c Universidade Estadual de Novosibirsk, 211 c Belkheeva R. K., 211

3 1. Expansão em série de Fourier de uma função periódica 2π Definição. A série de Fourier da função f(x) é a série funcional a 2 + (a n cosnx + b n sen nx), (1) onde os coeficientes a n, b n são calculados pelas fórmulas: a n = 1 π b n = 1 π f (x) cosnxdx, n = , 1,..., (2) f(x) sen nxdx, n = 1, 2,.... (3) As fórmulas (2) (3) são chamadas de fórmulas de Euler Fourier . O fato da função f(x) corresponder à série de Fourier (1) é escrito como uma fórmula f(x) a 2 + (a n cosnx + b n sen nx) (4) e dizem que o lado direito da fórmula ( 4) é uma série formal de funções de Fourier f(x). Em outras palavras, a fórmula (4) significa apenas que os coeficientes a n, b n são encontrados pelas fórmulas (2), (3). 3

4 Definição. Uma função periódica 2π f(x) é chamada suave por partes se o intervalo [, π] contém um número finito de pontos = x< x 1 <... < x n = π таких, что в каждом открытом промежутке (x j, x j+1) функция f(x) непрерывно дифференцируема, а в каждой точке x j существуют конечные пределы слева и справа: f(x j) = lim h + f(x j h), f(x j +) = lim h + f(x j + h), (5) f(x j h) f(x j) f(x j + h) f(x j +) lim, lim. h + h h + h (6) Отметим, что последние два предела превратятся в односторонние производные после замены предельных значений f(x j) и f(x j +) значениями f(x j). Теорема о представимости кусочно-гладкой функции в точке своим рядом Фурье (теорема о поточечной сходимости). Ряд Фурье кусочно-гладкой 2π-периодической функции f(x) сходится в каждой точке x R, а его сумма равна числу f(x), если x точка непрерывности функции f(x), f(x +) + f(x) и равна числу, если x точка разрыва 2 функции f(x). ПРИМЕР 1. Нарисуем график, найдем ряд Фурье функции, заданной на промежутке [, π] формулой, f(x) = x, предполагая, что она имеет период 2π, и вычислим суммы 1 1 числовых рядов (2n + 1) 2, n 2. n= Решение. Построим график функции f(x). Получим кусочно-линейную непрерывную кривую с изломами в точках x = πk, k целое число (рис. 1). 4

5 Fig. 1. Gráfico da função f(x) nx + π n n 2 = 2 π (1) n 1 n 2 = b n = 1 π π = 2 π f(x) cosnxdx = cos nx cos n 2 = 4 πn2, para n ímpar, para n par, f(x ) sin nxdx = porque a função f(x) é par. Escrevemos a série formal de Fourier para a função f(x): f(x) π 2 4 π k= 5 cos (2k + 1)x (2k + 1) 2.

6 Descubra se a função f(x) é suave por partes. Como é contínuo, calculamos apenas os limites (6) nos pontos finais do intervalo x = ±π e no ponto de quebra x = : e f(π h) f(π) π h π lim = lim h + h h + h = 1, f(+ h) f(+) + h () lim = lim h + h h + h f(+ h) f(+) + h lim = lim = 1, h + h h + h = 1 , f(h) f () h () lim = lim = 1. h + h h + h Os limites existem e são finitos, portanto a função é suave por partes. Pelo teorema da convergência pontual, sua série de Fourier converge para o número f(x) em cada ponto, ou seja, f(x) = π 2 4 π k= cos (2k + 1) + x (2k + 1) 2 = = π 2 4 (cosx + 19 π cos 3x) cos 5x (7) As Figuras 2 e 3 mostram o caráter da aproximação das somas parciais da série de Fourier S n (x), onde S n (x) = a n 2 + (a k coskx + b k sen kx), k=1, para a função f(x) no intervalo [, π] . 6

7 Fig. Fig. 2. Gráfico da função f(x) com gráficos sobrepostos de somas parciais S (x) = a 2 e S 1(x) = a 2 + a 1 cos x 3. Gráfico da função f (x) com um gráfico de soma parcial sobreposto S 99 (x) \u003d a 2 + a 1 cos x + + a 99 cos 99x 7

8 Substituindo em (7) x = obtemos: = π 2 4 π k= 1 (2k + 1) 2, de onde encontramos a soma da série numérica: = π2 8. Conhecendo a soma desta série, é fácil encontrar a seguinte soma Temos: S = ( ) S = ()= π S, portanto S = π2 6, isto é, 1 n = π A soma desta famosa série foi encontrada pela primeira vez por Leonhard Euler. É freqüentemente encontrado em análises matemáticas e suas aplicações. EXEMPLO 2. Desenhe um gráfico, encontre a série de Fourier da função dada pela fórmula f(x) = x para x< π, предполагая, что она имеет период 2π, и вычислим суммы числовых (1) n) рядов + n= ((2n + 1,) (k k + 1) Решение. График функции f(x) приведен на рис. 4. 8

9 Fig. 4. Gráfico da função f(x) A função f(x) é continuamente diferenciável no intervalo (, π). Nos pontos x = ±π, tem limites finitos (5): f() =, f(π) = π. Além disso, existem limites finitos (6): f(+ h) f(+) lim = 1 e h + h f(π h) f(π +) lim = 1. h + h Portanto, f(x) é função suave por partes. Como a função f(x) é ímpar, então a n =. Os coeficientes b n são encontrados por integração por partes: b n = 1 π f(x) sen πnxdx= 1 [ x cosnx π πn + 1 n = 1 πn [(1)n π + (1) n π] = 2(1 ) n+ 1. n Vamos compor a série formal de Fourier da função 2(1) n+1 f(x) sen nx. n 9 cosnxdx] =

10 De acordo com o teorema da convergência pontual para uma função periódica 2π suave por partes, a série de Fourier da função f(x) converge para a soma: 2(1) n+1 sin nx = n f(x) = x se π< x < π, = f(π) + f(π +) 2 =, если x = π, (8) f() + f(+) =, если x =. 2 На рис. 5 8 показан характер приближения частичных сумм S n (x) ряда Фурье к функции f(x). Рис. 5. График функции f(x) с наложенным на него графиком частичной суммы S 1 (x) = a 2 + a 1 cos x 1

11 Fig. Fig. 6. Gráfico da função f(x) com o gráfico da soma parcial S 2 (x) sobreposto a ele. 7. Gráfico da função f(x) com o gráfico da soma parcial S 3 (x) 11 sobreposto a ele

12 Fig. 8. Gráfico da função f(x) com o gráfico da soma parcial S 99 (x) sobreposta.Usamos a série de Fourier obtida para encontrar as somas de duas séries numéricas. Colocamos (8) x = π/2. Então 2 () +... = π 2, ou = n= (1) n 2n + 1 = π 4. Encontramos facilmente a soma da conhecida série de Leibniz. Colocando x = π/3 em (8), encontramos () +... = π 2 3, ou (1+ 1) () (k) 3π +...= 3k

13 EXEMPLO 3. Desenhe um gráfico, encontre a série de Fourier da função f(x) = sen x, supondo que ela tenha um período de 2π, e 1 calcule a soma da série de números 4n 2 1. Solução. O gráfico da função f(x) é mostrado na fig. 9. Obviamente, f(x) = sen x é uma função contínua par com período π. Mas 2π também é o período da função f(x). Arroz. 9. Gráfico da função f(x) Vamos calcular os coeficientes de Fourier. Tudo b n = porque a função é par. Usando fórmulas trigonométricas, calculamos a n para n 1: a n = 1 π = 1 π sen x cosnxdx = 2 π sen x cosnxdx = (sen(1 + n)x sen(1 n)x) dx = = 1 () π cos( 1 + n)x cos(1 n)x + = 2 () 1 + (1) n = π 1 + n 1 n π 1 n 2 ( 4 1 se n = 2k, = π n 2 1 se n = 2k

14 Este cálculo não nos permite encontrar o coeficiente a 1 porque em n = 1 o denominador vai para zero. Portanto, calculamos o coeficiente a 1 diretamente: a 1 = 1 π sen x cosxdx =. Como f(x) é continuamente diferenciável em (,) e (, π) e nos pontos kπ, (k é um número inteiro), existem limites finitos (5) e (6), a série de Fourier da função converge para em todos os pontos: = 2 π 4 π senx = 2 π 4 π cos 2nx 4n 2 1 = (1 1 cos 2x cos 4x + 1) cos 6x 1. Gráfico da função f(x) com o gráfico da soma parcial S(x) sobreposto a ele 14

15 Fig. Fig. 11. Gráfico da função f(x) com o gráfico da soma parcial S 1 (x) sobreposto a ele. Fig. 12. Gráfico da função f(x) com o gráfico da soma parcial S 2 (x) sobreposto a ele. 13. Gráfico da função f(x) com o gráfico da soma parcial S 99 (x) 15 sobreposto a ele

16 1 Calcule a soma da série numérica. Para fazer isso, colocamos 4n 2 1 em (9) x =. Então cosnx = 1 para todo n = 1, 2,... e Portanto, 2 π 4 π 1 4n 2 1 =. 1 4n 2 1 = = 1 2. EXEMPLO 4. Vamos provar que se uma função contínua suave por partes f(x) satisfaz a condição f(x π) = f(x) para todo x (isto é, é π-periódico) , então a 2n 1 = b 2n 1 = para todo n 1, e vice-versa, se a 2n 1 = b 2n 1 = para todo n 1, então f(x) é π-periódico. Solução. Seja a função f(x) π-periódica. Vamos calcular seus coeficientes de Fourier a 2n 1 e b 2n 1: = 1 π (a 2n 1 = 1 π f(x) cos(2n 1)xdx + f(x) cos(2n 1)xdx =) f(x ) cos(2n 1)xdx. Na primeira integral fazemos a mudança de variável x = t π : f(x) cos(2n 1)xdx = f(t π) cos(2n 1)(t + π) dt. 16

17 Usando o fato de que cos(2n 1)(t + π) = cos(2n 1)t e f(t π) = f(t), obtemos: a 2n 1 = 1 π (f(x) cos( 2n 1)x dx+) f(x) cos(2n 1)x dx =. Prova-se similarmente que b 2n 1 =. Reciprocamente, seja a 2n 1 = b 2n 1 =. Como a função f(x) é contínua, então, pelo teorema da representabilidade de uma função em um ponto por sua série de Fourier, temos Então f(x π) = f(x) = (a 2n cos 2nx + b 2n sen 2nx). (a2n cos 2n(x π) + b 2n sen 2n(x π)) = (a2n cos 2nx + b 2n sen 2nx) = f(x), o que significa que f(x) é uma função periódica π. EXEMPLO 5. Vamos provar que se uma função suave por partes f(x) satisfaz a condição f(x) = f(x) para todo x, então a = e a 2n = b 2n = para todo n 1, e vice-versa , se a = a 2n = b 2n =, então f(x π) = f(x) para todo x. Solução. Deixe a função f(x) satisfazer a condição f(x π) = f(x). Calculemos seus coeficientes de Fourier: 17

18 = 1 π (a n = 1 π f(x) cos nxdx + f(x) cosnxdx =) f(x) cosnxdx. Na primeira integral fazemos a mudança de variável x = t π. Então f(x) cosnxdx = f(t π) cosn(t π) dt. Usando o fato de que cos n(t π) = (1) n cosnt e f(t π) = f(t), obtemos: a n = 1 π ((1) n) f(t) cosnt dt = se n par, = 2 π f(t) cos nt dt, se n for ímpar. π Prova-se similarmente que b 2n =. Inversamente, seja a = a 2n = b 2n =, para todo n 1. Como a função f(x) é contínua, então, pelo teorema da representabilidade de uma função em um ponto, sua série de Fourier satisfaz a igualdade f( x) = (a 2n 1 cos ( 2n 1)x + b 2n 1 sen (2n 1)x). 18

19 Então = f(x π) = = = f(x). EXEMPLO 6. Vamos estudar como estender a função f(x) integrável no intervalo [, π/2] ao intervalo [, π], de modo que sua série de Fourier tenha a forma: a 2n 1 cos(2n 1) x. (1) Solução. Deixe o gráfico da função ter a forma mostrada na Fig. 14. Visto que na série (1) a = a 2n = b 2n = para todo n, segue-se do Exemplo 5 que a função f(x) deve satisfazer a igualdade f(x π) = f(x) para todo x. Esta observação fornece uma maneira de estender a função f(x) ao intervalo [, /2] : f(x) = f(x+π), fig. 15. Pelo fato de a série (1) conter apenas cossenos, concluímos que a função contínua f (x) deve ser par (isto é, seu gráfico deve ser simétrico em relação ao eixo Oy), Fig.

20 Fig. 14. Gráfico da função f(x) 15. Gráfico da continuação da função f(x) no intervalo [, /2] 2

21 Assim, a função desejada tem a forma mostrada na fig. 16. Fig. 16. Gráfico da continuação da função f(x) no intervalo [, π] Resumindo, concluímos que a função deve continuar da seguinte forma: f(x) = f(x), f(π x) = f(x), isto é intervalo [π/2, π], o gráfico da função f(x) é centralmente simétrico em relação ao ponto (π/2,), e no intervalo [, π], seu gráfico é simétrica em relação ao eixo Oy. 21

22 GENERALIZAÇÃO DOS EXEMPLOS 3 6 Seja l >. Considere duas condições: a) f(l x) = f(x); b) f(l + x) = f(x), x [, l/2]. Do ponto de vista geométrico, a condição (a) significa que o gráfico da função f(x) é simétrico em relação à reta vertical x = l/2, e a condição (b) que o gráfico f(x) é centralmente simétrico em relação ao ponto (l/2;) no eixo abscissa. Então as seguintes afirmações são verdadeiras: 1) se a função f(x) é par e a condição (a) é satisfeita, então b 1 = b 2 = b 3 =... =, a 1 = a 3 = a 5 = ... = ; 2) se a função f(x) for par e a condição (b) for satisfeita, então b 1 = b 2 = b 3 =... =, a = a 2 = a 4 =... = ; 3) se a função f(x) for ímpar e a condição (a) for satisfeita, então a = a 1 = a 2 =... =, b 2 = b 4 = b 6 =... = ; 4) se a função f(x) for ímpar e a condição (b) for satisfeita, então a = a 1 = a 2 =... =, b 1 = b 3 = b 5 =... =. PROBLEMAS Nos problemas 1 7 desenhe gráficos e encontre a série de Fourier para as funções (supondo que elas tenham um período de 2π: se< x <, 1. f(x) = 1, если < x < π. 1, если < x < /2, 2. f(x) =, если /2 < x < π/2, 1, если π/2 < x < π. 3. f(x) = x 2 (< x < π). 4. f(x) = x 3 (< x < π). { π/2 + x, если < x <, 5. f(x) = π/2 x, если < x < π. 22

23 ( 1 se /2< x < π/2, 6. f(x) = 1, если π/2 < x < 3π/2. {, если < x <, 7. f(x) = sin x, если < x < π. 8. Как следует продолжить интегрируемую на промежутке [, π/2] функцию f(x) на промежуток [, π], чтобы ее ряд Фурье имел вид: b 2n 1 sin (2n 1)x? Ответы sin(2n 1)x sin(2n + 1)x. π 2n 1 π 2n + 1 n= 3. 1 (1) n () 12 3 π2 + 4 cosnx. 4. (1) n n 2 n 2π2 sin nx. 3 n 5. 4 cos(2n + 1)x π (2n + 1) (1) n cos(2n + 1)x. π 2n + 1 n= n= 7. 1 π sin x 2 cos 2nx. 8. Функцию следует продолжить следующим образом: f(x) = f(x), f(π x) = f(x), π 4n 2 1 то есть на промежутке [, π], график функции f(x) будет симметричен относительно вертикальной прямой x = π/2, на промежутке [, π] ее график центрально симметричен относительно точки (,). 23

24 2. Expansão de uma função dada no intervalo [, π] apenas em termos de senos ou apenas em termos de cossenos Seja uma função f dada no intervalo [, π]. Para expandi-lo neste intervalo em uma série de Fourier, primeiro estendemos f no intervalo [, π] de maneira arbitrária e, em seguida, usamos as fórmulas de Euler Fourier. A arbitrariedade na continuação de uma função leva ao fato de que para uma mesma função f: [, π] R podemos obter diferentes séries de Fourier. Mas é possível usar essa arbitrariedade de modo a obter uma expansão apenas em senos ou apenas em cossenos: no primeiro caso, basta continuar f de maneira ímpar e, no segundo, de maneira par. Algoritmo de solução 1. Continue a função de maneira ímpar (par) em (,) e, periodicamente, com um período de 2π, continue a função em todo o eixo. 2. Calcule os coeficientes de Fourier. 3. Componha a série de Fourier da função f(x). 4. Verifique as condições de convergência da série. 5. Especifique a função para a qual esta série irá convergir. EXEMPLO 7. Expanda a função f(x) = cosx,< x < π, в ряд Фурье только по синусам. Решение. Продолжим функцию нечетным образом на (,) (т. е. так, чтобы равенство f(x) = f(x) выполнялось для всех x (, π)), а затем периодически с периодом 2π на всю ось. Получим функцию f (x), график которой приведен на рис

25 Fig. 17. Gráfico da função contínua Obviamente, a função f(x) é suave por partes. Vamos calcular os coeficientes de Fourier: a n = para todo n porque a função f(x) é ímpar. Se n 1, então b n = 2 π f(x) sen πnxdx = 2 π cosx sen nxdx = = 2 π dx = = 2 π cos (n + 1) x cos (n 1) x + = π n + 1 n 1 = 1 (1) n (1)n 1 1 = π n + 1 n 1 = 1 se n = 2 k + 1, (1)n+1 (n 1) + (n + 1) = π ( n + 1)(n 1) 2 2n se n = 2k. π n 2 1 Para n = 1 nos cálculos anteriores, o denominador desaparece, então o coeficiente b 1 pode ser calculado diretamente.

26 Essencialmente: b 1 = 2 π cosx sen xdx =. Componha a série de Fourier da função f (x) : f (x) 8 π k=1 k 4k 2 1 sen 2kx. Como a função f (x) é suave por partes, então, pelo teorema da convergência pontual, a série de Fourier da função f (x) converge para a soma cosx se π< x <, S(x) =, если x =, x = ±π, cosx, если < x < π. В результате функция f(x) = cosx, заданная на промежутке (, π), выражена через синусы: cosx = 8 π k=1 k 4k 2 1 sin 2kx, x (, π). Рис демонстрируют постепенное приближение частичных сумм S 1 (x), S 2 (x), S 3 (x) к разрывной функции f (x). 26

27 Fig. Fig. 18. Gráfico da função f (x) com o gráfico da soma parcial S 1 (x) sobreposto a ele. 19. Gráfico da função f(x) com o gráfico da soma parcial S 2 (x) sobreposto a ele 27

28 Fig. Fig. 2. Gráfico da função f(x) com o gráfico da soma parcial S 3 (x) sobreposto a ele. 21 mostra gráficos da função f (x) e sua soma parcial S 99 (x). Arroz. 21. Gráfico da função f (x) com um gráfico da soma parcial S 99 (x) 28 sobreposto a ele

29 EXEMPLO 8. Vamos expandir a função f(x) = e ax, a >, x [, π], em uma série de Fourier apenas em cossenos. Solução. Continuamos a função de maneira uniforme para (,) (ou seja, de modo que a igualdade f(x) = f(x) seja válida para todo x (, π)), e então periodicamente com um período de 2π para todo o real eixo. Obtemos a função f (x), cujo gráfico é mostrado na Fig. 22. Função f(x) nos pontos 22. O gráfico da função contínua f (x) x = kπ, k é um número inteiro, tem dobras. Calculemos os coeficientes de Fourier: b n =, pois f(x) é par. Integrando por partes, obtemos 29

30 a n = 2 π a = 2 π = 2 cosnxd(e ax) = 2 πa e ax dx = 2 π a (eaπ 1), f(x) cos πnxdx = 2 π πa eax cosnx = 2 πa (eaπ cosnπ 1 ) + 2n πa 2 π e ax cos nxdx = + 2n e ax sin nxdx = πa sin nxde ax = = 2 π a (eaπ cos n π 1) + 2n π sen nx π a 2eax 2n2 e ax cos nxdx = 2 π a 2 π a (eaπ cos n π 1) n2 a a n. 2 Portanto, a n = 2a e aπ cos n π 1. π a 2 + n 2 Como f (x) é contínua, de acordo com o teorema da convergência pontual, sua série de Fourier converge para f (x). Assim, para todo x [, π] temos f(x) = 1 π a (eaπ 1)+ 2a π k=1 e aπ (1) k 1 a 2 + k 2 coskx (x π). As figuras demonstram a aproximação gradual das somas parciais da série de Fourier a uma dada função descontínua. 3

31 Fig. 23. Gráficos das funções f(x) e S(x) 24. Gráficos das funções f (x) e S 1 (x) 25. Gráficos das funções f(x) e S 2 (x) 26. Gráficos das funções f(x) e S 3 (x) 31

32 Fig. 27. Gráficos das funções f (x) e S 4 (x) 28. Gráficos das funções f (x) e S 99 (x) PROBLEMA 9. Expandir a função f (x) = cos x, x π, em uma série de Fourier apenas em cossenos. 1. Expanda a função f (x) \u003d e ax, a >, x π, em uma série de Fourier apenas em termos de senos. 11. Expanda a função f (x) \u003d x 2, x π, em uma série de Fourier apenas em senos. 12. Expanda a função f (x) \u003d sen ax, x π, em uma série de Fourier apenas em termos de cossenos. 13. Expanda a função f (x) \u003d x sen x, x π, em uma série de Fourier apenas em senos. Respostas 9. cosx = cosx. 1. e ax = 2 [ 1 (1) k e aπ] k sen kx. π a 2 + k2 k=1 11. x 2 2 [ π 2 (1) n 1 π n + 2 ] n 3 ((1)n 1) sen nx. 32

33 12. Se a não é um inteiro, então sin ax = 1 cosaπ (1 + +2a cos 2nx ) + π a 2 (2n) 2 +2a 1 + cosaπ cos(2n 1)x π a 2 (2n 1) 2; se a = 2m é um número par, então sin 2mx = 8m cos(2n 1)x π (2m) 2 (2n 1) 2; se a = 2m 1 é um número ímpar positivo, então sin(2m 1)x = 2 ( cos 2nx ) 1 + 2(2m 1). π (2m 1) 2 (2n) π 16 n sen x sen 2nx. 2 π (4n 2 1) 2 3. Série de Fourier de uma função com período arbitrário Assuma que a função f(x) é definida no intervalo [ l, l], l >. Substituindo x = ly, y π, obtemos a função g(y) = f(ly/π) definida no intervalo π [, π]. Esta função g(y) corresponde à (formal) série de Fourier () ly f = g(y) a π 2 + (a n cosny + b n sen ny), cujos coeficientes são encontrados pelas fórmulas de Euler Fourier: a n = 1 π g(y) cosny dy = 1 π f (ly π) cos ny dy, n =, 1, 2,..., 33

34 b n = 1 π g(y) sinny dy = 1 π f () ly sin ny dy, n = 1, 2,.... π l, obtemos uma série trigonométrica ligeiramente modificada para a função f(x): onde f(x) a 2 + a n = 1 l b n = 1 l l l l l (a n cos πnx l f(x) cos πnx l f(x) sin πnx l + b n sen πnx), (11) l dx, n =, 1, 2 ,..., (12) dx, n = 1, 2,.... (13) Diz-se que as fórmulas (11) (13) definem a expansão em uma série de Fourier de uma função com um período arbitrário. EXEMPLO 9. Encontre a série de Fourier da função dada no intervalo (l, l) pela expressão ( A se l< x, f(x) = B, если < x < l, считая, что она периодична с периодом 2l. Решение. Продолжим функцию периодически, с периодом 2l, на всю ось. Получим функцию f (x), кусочно-постоянную в промежутках (l + 2kl, l + 2kl), и претерпевающую разрывы первого рода в точках x = lk, k целое число. Ее коэффициенты Фурье вычисляются по формулам (12) и (13): 34

35 a = 1 l l f(x) dx = 1 l A dx + 1 l l B dx = A + B, l l a n = 1 l l l f(x) cos πnx l dx = = 1 l = 1 l l A cos πnx l = A + B π n l b n = 1 l dx + 1 l l B cos πnx l sin πn = se n, l l A sin πnx l f(x) sin πnx l dx + 1 l l dx = B sin πnx l = B A (1 cosπn). πn Componha a série de Fourier da função f(x): f(x) A + B π (B A Dado que cosπn = (1) n, então n dx = dx = (1 cosπn) sin πnx). l para n = 2k obtemos b n = b 2k =, para n = 2k 1 b n = b 2k 1 = 35 2(B A) π(2k 1).

36 Portanto f(x) A + B (B A) π (sin πx + 1 3πx sin + 1 5πx sin +... l 3 l 5 l De acordo com o teorema da convergência pontual, a série de Fourier da função f(x) converge para a soma A, se l< x, S(x) = A + B, если x =, x = ±l, 2 B, если < x < l. Придавая параметрам l, A, B конкретные значения получим разложения в ряд Фурье различных функций. Пусть l = π, A =, B = 3π. На рис. 29 приведены графики первых пяти членов ряда, функции f (x) и частичной суммы S 7 (x) = a 2 + b 1 sin x b 7 sin 7x. Величина a является средним значением функции на промежутке. Обратим внимание на то, что с возрастанием ча- 2 стоты гармоники ее амплитуда уменьшается. Для наглядности графики трех высших гармоник сдвинуты по вертикали. На рис. 3 приведен график функции f(x) и частичной суммы S 99 (x) = a 2 + b 1 sin x b 99 sin 99x. Для наглядности на рис. 31 приведен тот же график в другом масштабе. Последние два графика иллюстрируют явление Гиббса. 36).

37 Fig. 29. Gráfico da função f (x) com gráficos sobrepostos dos harmônicos S (x) = a 2 e S 1 (x) = b 1 senx. Para maior clareza, os gráficos dos três harmônicos superiores S 3 (x) \u003d b 3 sin 3πx, S l 5 (x) \u003d b 5 sin 5πx l e S 7 (x) \u003d b 7 sin 7πx são deslocados verticalmente para cima l 37

38 Fig. Fig. 3. Gráfico da função f(x) com o gráfico da soma parcial S 99 (x) sobreposto a ele. 31. Fragmento da fig. 3 em outra escala 38

39 PROBLEMAS Nos problemas, expanda as funções especificadas na série de Fourier em intervalos dados. 14. f(x) = x 1, (1, 1). 15. f(x) = ch2x, (2, 2] f(x) = x (1 x), (1, 1). 17. f(x) = cos π x, [ 1, 1] f(x ) = sen π x, (1, 1).( 2 1 se 1< x < 1, 19. f(x) = 2l = 4., если 1 < x < 3; x, если x 1, 2. f(x) = 1, если 1 < x < 2, 2l = 3. { 3 x, если 2 x < 3;, если ωx, 21. f(x) = 2l = 2π/ω. sin ωx, если ωx π; Разложить в ряды Фурье: а) только по косинусам; б) только по синусам указанные функции в заданных промежутках (, l) { 22. f(x) = { 23. f(x) = ax, если < x < l/2, a(l x), если l/2 < x < l. 1, если < x 1, 2 x, если 1 x 2. Ответы 14. f(x) = 4 cos(2n 1)πx. π 2 (2n 1) f(x) = sh sh4 (1) n nπx cos 16 + π 2 n f(x) = cos 2nπx. π 2 n f(x) = 2 π + 8 π (1) n n 1 4n 2 cosnπx. 39

40 18. f(x) = 8 (1) n n sen nπx. π 1 4n (1) n 2n + 1 cos πx. π 2n πn 2πnx π 2 sen2 cos n π sen ωx 2 cos 2nωx π 4n 2 1. (l 22. a) f(x) = al 4 2) 1 (4n 2)πx cos, π 2 (2n 1) 2 l b) f(x) = 4al (1) n 1 (2n 1) πx sen. π 2 (2n 1) 2 l 23. a) f(x) = (cos π π 2 2 x 2 2 cos 2π 2 2 x cos 3π 2 2 x cos 5π), 2 2 x... b) f( x) = 4 (sin π π 2 2 x 1 3 sin 3π)+ 2 2 x (sin π π 2 x cos 2π) 2 x Forma complexa da Decomposição da série de Fourier f(x) = c n e inx, onde c n = 1 2π f (x)e inx dx, n = ±1, ±2,..., é chamada de forma complexa da série de Fourier. A função se expande em uma série de Fourier complexa nas mesmas condições em que se expande em uma série de Fourier real. 4

41 EXEMPLO 1. Encontre a série de Fourier na forma complexa da função dada pela fórmula f(x) = e ax no intervalo [, π), onde a é um número real. Solução. Calculemos os coeficientes: = c n = 1 2π f(x)e inx dx = 1 2π e (a in)x dx = 1 ((1) n e aπ (1) n e aπ) = (1)n shaπ. 2π(a in) π(a in) A série complexa de Fourier da função f tem a forma f(x) sh aπ π n= (1) n a in einx. Verifiquemos que a função f(x) é suave por partes: no intervalo (, π) é continuamente diferenciável, e nos pontos x = ±π existem limites finitos (5), (6) lim h + ea( +h) = e aπ, lim h + ea(π h) = e aπ, e a(+h) e a(+) lim h + h = ae aπ e a(π h) e a(π), lim h + h = ae aπ. Portanto, a função f(x) pode ser representada por uma série de Fourier sh aπ π n= (1) n a em einx, que converge para a soma: ( e S(x) = ax se π< x < π, ch a, если x = ±π. 41

42 EXEMPLO 11. Encontre a série de Fourier na forma complexa e real da função dada pela fórmula f(x) = 1 a 2 1 2a cosx + a2, onde a< 1, a R. Решение. Функция f(x) является четной, поэтому для всех n b n =, а a n = 2 π f(x) cosnxdx = 2 (1 a2) π cos nxdx 1 2a cosx + a 2. Не будем вычислять такой сложный интеграл, а применим следующий прием: 1. используя формулы Эйлера sin x = eix e ix 2i = z z 1, cosx = eix + e ix 2i 2 = z + z 1, 2 где z = e ix, преобразуем f(x) к рациональной функции комплексной переменной z; 2. полученную рациональную функцию разложим на простейшие дроби; 3. разложим простейшую дробь по формуле геометрической прогрессии; 4. упростим полученную формулу. Итак, по формулам Эйлера получаем = f(x) = 1 a 2 1 a(z + z 1) + a 2 = (a 2 1)z (z a)(z a 1) = a z a az. (14) 42

43 Lembre-se que a soma de uma progressão geométrica infinita com denominador q (q< 1) вычисляется по формуле: + n= q n = 1 1 q. Эта формула верна как для вещественных, так и для комплексных чисел. Поскольку az = a < 1 и a/z = a < 1, то az = + a n z n = a n e inx, a z a = a z 1 1 a/z = a z n= + n= a n z = + n n= n= a n+1 z = + a n+1 e i(n+1)x. n+1 После замены переменной (n + 1) = k, < k < 1, получим: 1 a z a = a k e ikx. Следовательно, f(x) + n= k= c n e inx, где c n = n= { a n, если n, a n, если n <, то есть c n = a n. Поскольку функция f(x) непрерывна, то в силу теоремы о поточечной сходимости имеет место равенство: f(x) = + n= a n e inx. Тем самым мы разложили функцию f(x) в ряд Фурье в комплексной форме. 43

44 Agora vamos encontrar a série de Fourier na forma real. Para fazer isso, agrupamos os termos com números n e n para n: a n e inx + a n e inx = 2a neinx + e inx Como c = 1, então 2 = 2a n cos nx. f(x) = 1 a 2 1 2a cosx + a = a n cosnx. 2 Esta é uma série de Fourier na forma real da função f(x). Assim, sem calcular uma única integral, encontramos a série de Fourier da função. Ao fazer isso, calculamos uma integral rígida dependendo do parâmetro cos nxdx 1 2a cosx + a = 2 π an 2 1 a2, a< 1. (15) ПРИМЕР 12. Найдем ряд Фурье в комплексной и вещественной форме функции, заданной формулой a sin x f(x) = 1 2a cosx + a2, a < 1, a R. Решение. Функция f(x) является нечетной, поэтому для всех n a n = и b n = 2 π f(x) sin nxdx = 2a π sin x sin nxdx 1 2a cosx + a 2. Чтобы записать ряд Фурье нужно вычислить сложные интегралы или воспользоваться приемом, описанным выше. Поступим вторым способом: 44

45 a(z z 1) f(x) = 2i (1 a(z z 1) + a 2) = i 2 + i (a + a 1)z 2 2 (z a)(z a 1) = = i 2 + i () a 2 z a + a 1. z a 1 Expandimos cada uma das frações simples de acordo com a fórmula de progressão geométrica: + a z a = a 1 z 1 a = a a n z z n, n= z a 1 z a = az = a n z n. n= Isso é possível porque az = a/z = a< 1. Значит + ia n /2, если n <, f(x) c n e inx, где c n =, если n =, n= ia n /2, если n >, ou, mais brevemente, c n = 1 2i a n sgnn. Assim, a série de Fourier na forma complexa é encontrada. Agrupando os termos com números n e n, obtemos a série de Fourier da função na forma real: = f(x) = + a sen x 1 2a cosx + a + 2 (1 2i an e inx 1 2i an e inx n= +) = c n e inx = a n sen nx. Novamente, conseguimos calcular a seguinte integral complexa: sen x sen nxdx 1 2a cosx + a 2 = π an 1. (16) 45

46 PROBLEMA 24. Usando (15), calcule a integral cos nxdx 1 2a cosx + a 2 para reais a, a > Usando (16), calcule a integral sen x sen nxdx para reais a, a > a cosx + a2 Em problemas , encontre a série Fourier na forma complexa para funções. 26. f(x) = sgn x, π< x < π. 27. f(x) = ln(1 2a cosx + a 2), a < 1. 1 a cosx 28. f(x) = 1 2a cosx + a2, a < Докажите, что функция f, определенная в промежутке [, π], вещественнозначна, если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является четной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n = ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является нечетной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2,.... Ответы 1 2π 24. a n a π a n i + e 2inx, где подразумевается, что слагаемое, соответствующее n =, пропущено. π n n= a n n cosnx. 28. a n cosnx. n= 46

47 5. Teorema da igualdade de Lyapunov (a igualdade de Lyapunov). Seja uma função f: [, π] R tal que f 2 (x) dx< +, и пусть a n, b n ее коэффициенты Фурье. Тогда справедливо равенство, a (a 2 n + b2 n) = 1 π называемое равенством Ляпунова. f 2 (x) dx, ПРИМЕР 13. Напишем равенство Ляпунова для функции { 1, если x < a, f(x) =, если a < x < π и найдем с его помощью суммы числовых рядов + sin 2 na n 2 и + Решение. Очевидно, 1 (2n 1) 2. 1 π f 2 (x) dx = 1 π a a dx = 2a π. Так как f(x) четная функция, то для всех n имеем b n =, a = 2 π f(x) dx = 2 π a dx = 2a π, 47

48 a n = 2 π f(x) cosnxdx = 2 π a cos nxdx = 2 sin na πn. Portanto, a igualdade de Lyapunov para a função f(x) assume a forma: 2 a 2 π + 4 sin 2 na = 2a 2 π 2 n 2 π. Da última igualdade para a π encontramos sin 2 na n 2 = a(π a) 2 Assumindo a = π 2, obtemos sin2 na = 1 para n = 2k 1 e sin 2 na = para n = 2k. Portanto, k=1 1 (2k 1) 2 = π2 8. EXEMPLO 14. Vamos escrever a igualdade de Lyapunov para a função f(x) = x cosx, x [, π], e usá-la para encontrar a soma do número série (4n 2 + 1) 2 (4n 2 1) 4. 1 π Solução. Cálculos diretos fornecem = π π f 2 (x) dx = 1 π x 2 cos 2 xdx = 1 π x sin 2xdx = π π x cos x = π x 21 + cos 2x dx = 2 π 1 4π cos 2xdx =

49 Como f(x) é uma função par, então para todo n temos b n =, a n = 2 π = 1 π 1 = π(n + 1) = f(x) cosnxdx = 2 π 1 cos(n + 1 )x π (n + 1) 2 x cosxcosnxdx = x (cos(n + 1)x + cos(n 1)x) dx = 1 π sin(n + 1)xdx sin(n 1)xdx = π(n 1) π π 1 + cos(n 1)x = π(n 1) 2 1 (= (1) (n+1) 1) 1 (+ (1) (n+1) 1) = π(n + 1) 2 π(n 1) 2 () = (1)(n+1) 1 1 π (n + 1) + 1 = 2 (n 1) 2 = 2 (1)(n+1) 1 n k π (n 2 1) = π (4k 2 1) 2 se n = 2k, 2 se n = 2k + 1. O coeficiente a 1 deve ser calculado separadamente, pois na fórmula geral para n = 1 o denominador da fração desaparece . = 1 π a 1 = 2 π f(x) cosxdx = 2 π x(1 + cos 2x)dx = π 2 1 2π 49 x cos 2 xdx = sin 2xdx = π 2.

50 Assim, a igualdade de Lyapunov para a função f(x) tem a forma: 8 π + π (4n 2 + 1) 2 π 2 (4n 2 1) = π 2 1) = π π PROBLEMA 32. Escreva a igualdade de Lyapunov para a função ( x f(x) = 2 πx se x< π, x 2 πx, если π < x. 33. Напишите равенства Ляпунова для функций f(x) = cos ax и g(x) = sin ax, x [, π]. 34. Используя результат предыдущей задачи и предполагая, что a не является целым числом, выведите следующие классические разложения функций πctgaπ и (π/ sin aπ) 2 по рациональным функциям: πctgaπ = 1 a + + 2a a 2 n 2, (π) = sin aπ (a n) 2. n= 35. Выведите комплексную форму обобщенного равенства Ляпунова. 36. Покажите, что комплексная форма равенства Ляпунова справедлива не только для вещественнозначных функций, но и для комплекснозначных функций. 5

51 π (2n + 1) = π sen 2απ 2απ = 2sin2 απ α 2 π 2 Respostas + 4 sin2 απ π 2 α 2 (α 2 n 2) 2; sin 2απ 1 2απ = απ n 2 4sin2 π 2 (α 2 n 2) 2. 1 π 35. f(x)g(x) dx= c n d n, onde c n é o coeficiente de Fourier 2π de f(x) e d n são as funções do coeficiente de Fourier g(x). 6. Diferenciação da série de Fourier Seja f: R R uma função 2π-periódica continuamente diferenciável. Sua série de Fourier tem a forma: f(x) = a 2 + (a n cos nx + b n sen nx). A derivada f (x) desta função será uma função contínua e 2π periódica, para a qual uma série formal de Fourier pode ser escrita: f (x) a 2 + (a n cos nx + b n sen nx), onde a, a n , b n, n = 1 , 2,... Coeficientes de Fourier da função f (x). 51

52 Teorema (sobre a diferenciação termo a termo da série de Fourier). Sob as suposições acima, as igualdades a =, a n = nb n, b n = na n, n 1 são verdadeiras EXEMPLO 15. Seja uma função suave por partes f(x) contínua no intervalo [, π]. Provemos que quando a condição f(x)dx = é satisfeita, a desigualdade 2 dx 2 dx, chamada desigualdade de Steklov, vale, e verificamos que a igualdade nela é realizada apenas para funções da forma f(x) = A cox. Em outras palavras, a desigualdade de Steklov dá condições sob as quais a pequenez da derivada (em rms) implica a pequenez da função (em rms). Solução. Vamos estender a função f(x) ao intervalo [, ] uniformemente. Denote a função estendida pelo mesmo símbolo f(x). Então a função contínua será contínua e suave por partes no intervalo [, π]. Como a função f(x) é contínua, então f 2 (x) é contínua no intervalo e 2 dx< +, следовательно, можно применить теорему Ляпунова, согласно которой имеет место равенство 1 π 2 dx = a () a 2 n + b 2 n. 52

53 Como a função contínua é par, então b n =, a = por condição. Conseqüentemente, a igualdade de Lyapunov assume a forma 1 π 2 dx = a 2 π n. (17) Vamos garantir que f (x) satisfaça a conclusão do teorema sobre a diferenciação termo a termo da série de Fourier, ou seja, que a =, a n = nb n, b n = na n, n 1. Deixe a derivada f (x) sofrer quebras nos pontos x 1, x 2,..., x N no intervalo [, π]. Denote x =, x N+1 = π. Vamos dividir o intervalo de integração [, π] em N +1 intervalos (x, x 1),..., (x N, x N+1), em cada um dos quais f(x) é continuamente diferenciável. Então, usando a propriedade de aditividade da integral e depois integrando por partes, obtemos: b n = 1 π = 1 π = 1 π f (x) sin nxdx = 1 π N f(x) sin nx j= N f(x ) sin nx j= x j+1 x j x j+1 x j n n π N j= x j+1 x j x j+1 x j f (x) sin nxdx = f(x) cosnxdx = f(x) cosnxdx = = 1 π [( f(x 1) sen nx 1 f(x) sen nx) + + (f(x 2) sennx 2 f(x 1) sen nx 1)

54 + (f(x N+1) sin nx N+1 f(x N) sin nx N)] na n = = 1 π na n = = 1 π na n = na n. x j+1 a = 1 f (x)dx = 1 N f (x)dx = π π j= x j = 1 N x j+1 f(x) π = 1 (f(π) f()) = . x j π j= Da mesma forma, obtemos a n = nb n. Mostramos que o teorema sobre a diferenciação termo a termo da série de Fourier para uma função periódica 2π contínua suave por partes cuja derivada no intervalo [, π] sofre descontinuidades do primeiro tipo é verdadeiro. Então f (x) a 2 + (a n cosnx + b n sen nx) = (na n) sen nx, pois a =, a n = nb n =, b n = na n, n = 1, 2,.... Porque 2dx< +, то по равенству Ляпунова 1 π 2 dx = 54 n 2 a 2 n. (18)

55 Como cada termo da série em (18) é maior ou igual ao termo correspondente da série em (17), então 2 dx 2 dx. Lembrando que f(x) é uma continuação par da função original, temos 2 dx 2 dx. O que prova a igualdade de Steklov. Agora vamos examinar para quais funções a igualdade vale na desigualdade de Steklov. Se para pelo menos um n 2, o coeficiente a n é diferente de zero, então a 2 n< na 2 n. Следовательно, равенство a 2 n = n 2 a 2 n возможно только если a n = для n 2. При этом a 1 = A может быть произвольным. Значит в неравенстве Стеклова равенство достигается только на функциях вида f(x) = A cosx. Отметим, что условие πa = f(x)dx = (19) существенно для выполнения неравенства Стеклова, ведь если условие (19) нарушено, то неравенство примет вид: a a 2 n n 2 a 2 n, а это не может быть верно при произвольном a. 55

56 PROBLEMAS 37. Seja uma função suave por partes f(x) contínua no intervalo [, π]. Prove que sob a condição f() = f(π) = a desigualdade 2 dx 2 dx, também chamada de desigualdade de Steklov, vale, e certifique-se de que a igualdade vale apenas para funções da forma f(x) = B sen x . 38. Seja uma função f contínua no intervalo [, π] e tenha nela (com a possível exceção de apenas um número finito de pontos) uma derivada quadrada integrável f(x). Prove que se as condições f() = f(π) e f(x) dx = forem satisfeitas, então a desigualdade 2 dx 2 dx, chamada desigualdade de Wirtinger, vale, e a igualdade nela ocorre apenas para funções do forma f(x) = A cosx + B senx. 56

57 7. Aplicação da série de Fourier para resolução de equações diferenciais parciais Ao estudar um objeto real (fenômenos naturais, processo de produção, sistema de controle, etc.), dois fatores se tornam significativos: o nível de conhecimento acumulado sobre o objeto em estudo e o grau de desenvolvimento do aparato matemático. No estágio atual da pesquisa científica, a seguinte cadeia foi desenvolvida: um fenômeno um modelo físico um modelo matemático. A formulação física (modelo) do problema é a seguinte: são identificadas as condições para o desenvolvimento do processo e os principais fatores que o influenciam. A formulação matemática (modelo) consiste em descrever os fatores e condições escolhidos na formulação física na forma de um sistema de equações (algébricas, diferenciais, integrais, etc.). Um problema é dito bem-posto se, em um determinado espaço funcional, a solução do problema existe, única e continuamente dependente das condições iniciais e de contorno. O modelo matemático não é idêntico ao objeto em consideração, mas é sua descrição aproximada. Derivação da equação das pequenas vibrações transversais livres da corda. Seguiremos o livro didático. Que as pontas do barbante sejam fixadas e o próprio barbante esticado. Se a corda for retirada do equilíbrio (por exemplo, puxando-a ou golpeando-a), a corda começará 57

58 hesitar. Vamos assumir que todos os pontos da corda se movem perpendicularmente à sua posição de equilíbrio (vibrações transversais), e a cada momento a corda está no mesmo plano. Tomemos um sistema de coordenadas retangulares xou neste plano. Então, se no instante inicial t = a corda estava localizada ao longo do eixo Ox, então u significará o desvio da corda da posição de equilíbrio, ou seja, a posição do ponto da corda com a abcissa x em um tempo arbitrário t corresponde ao valor da função u(x, t). Para cada valor fixo de t, o gráfico da função u(x, t) representa a forma da corda vibrante no tempo t (Fig. 32). Em um valor constante de x, a função u(x, t) dá a lei do movimento de um ponto com a abcissa x ao longo de uma linha reta paralela ao eixo Ou, a derivada u t é a velocidade desse movimento e o segundo derivada 2 u t 2 é a aceleração. Arroz. 32. Forças aplicadas a uma seção infinitamente pequena de uma corda Vamos escrever uma equação que a função u(x, t) deve satisfazer. Para fazer isso, fazemos algumas suposições mais simplificadoras. Assumiremos que a corda é absolutamente flexível.

59 tímido, ou seja, assumiremos que a corda não resiste à flexão; isso significa que as tensões que surgem na corda são sempre direcionadas tangencialmente ao seu perfil instantâneo. A corda é considerada elástica e sujeita à lei de Hooke; isso significa que a mudança na magnitude da força de tração é proporcional à mudança no comprimento da corda. Suponhamos que a corda seja homogênea; isto significa que sua densidade linear ρ é constante. Negligenciamos as forças externas. Isso significa que estamos considerando oscilações livres. Estudaremos apenas pequenas vibrações de uma corda. Se denotarmos por ϕ(x, t) o ângulo entre o eixo das abcissas e a tangente à corda no ponto com a abcissa x no tempo t, então a condição para pequenas oscilações é que o valor de ϕ 2 (x, t) pode ser negligenciado em comparação com ϕ (x, t), ou seja, ϕ 2. Como o ângulo ϕ é pequeno, então cos ϕ 1, ϕ sin ϕ tg ϕ u, portanto, o valor (u x x,) 2 também pode ser negligenciado. Segue-se imediatamente disso que, no processo de oscilação, podemos desprezar a mudança no comprimento de qualquer seção da corda. De fato, o comprimento de um pedaço de barbante M 1 M 2 projetado no intervalo do eixo x, onde x 2 = x 1 + x, é igual a l = x 2 x () 2 u dx x. x Vamos mostrar que, sob nossas hipóteses, o valor da força de tração T será constante ao longo de toda a corda. Para fazer isso, pegamos alguma parte da corda M 1 M 2 (Fig. 32) no tempo t e substituímos a ação das partes descartadas

60 kov pelas forças de tensão T 1 e T 2. Como, de acordo com a condição, todos os pontos da corda se movem paralelamente ao eixo Ou e não há forças externas, a soma das projeções das forças de tensão no eixo Ox deve ser igual a zero: T 1 cosϕ(x 1, t) + T 2 cosϕ(x 2, t) =. Portanto, devido à pequenez dos ângulos ϕ 1 = ϕ(x 1, t) e ϕ 2 = ϕ(x 2, t), concluímos que T 1 = T 2. Denote o valor geral de T 1 = T 2 por T. Agora calculamos a soma das projeções F u das mesmas forças no eixo Ou: F u = T sen ϕ(x 2, t) T sen ϕ(x 1, t). (2) Como para pequenos ângulos sin ϕ(x, t) tg ϕ(x, t) e tg ϕ(x, t) u(x, t)/ x, a equação (2) pode ser reescrita como F u T (tan ϕ(x 2, t) tan ϕ(x 1, t)) (u T x (x 2, t) u) x (x 1, t) x x T 2 u x 2(x 1, t) x . Como o ponto x 1 é escolhido arbitrariamente, então F u T 2 u x2(x, t) x. Depois de encontradas todas as forças que atuam na seção M 1 M 2, aplicamos a ela a segunda lei de Newton, segundo a qual o produto da massa pela aceleração é igual à soma de todas as forças atuantes. A massa de um pedaço de corda M 1 M 2 é igual a m = ρ l ρ x, e a aceleração é igual a 2 u(x, t). A equação t 2 de Newton assume a forma: 2 u t (x, t) x = u 2 α2 2 x2(x, t) x, onde α 2 = T ρ é um número positivo constante. 6

61 Reduzindo por x, obtemos 2 u t (x, t) = u 2 α2 2 x2(x, t). (21) Como resultado, obtivemos uma equação diferencial parcial homogênea linear de segunda ordem com coeficientes constantes. É chamada de equação de vibração de cordas ou equação de onda unidimensional. A equação (21) é essencialmente uma reformulação da lei de Newton e descreve o movimento de uma corda. Mas na formulação física do problema, havia requisitos de que as extremidades da corda fossem fixas e a posição da corda em algum ponto no tempo fosse conhecida. Escreveremos essas condições nas equações da seguinte forma: a) assumiremos que as extremidades da corda são fixadas nos pontos x = e x = l, ou seja, assumiremos que para todo t as relações u(, t) = , u(l, t ) = ; (22) b) assumiremos que no instante t = a posição da string coincide com o gráfico da função f(x), ou seja, assumiremos que para todo x [, l] a igualdade u(x, ) = f(x); (23) c) vamos supor que no instante t = o ponto da corda com a abcissa x é dada a velocidade g(x), ou seja, vamos supor que u(x,) = g(x). (24) t As relações (22) são chamadas de condições de contorno, e as relações (23) e (24) são chamadas de condições iniciais. Modelo matemático de pequena transversal livre 61

62 vibrações da corda é que é necessário resolver a equação (21) com as condições de contorno (22) e as condições iniciais (23) e (24) Solução da equação das pequenas vibrações transversais livres da corda pelo método de Fourier< t <, удовлетворяющие граничным условиям (22) и начальным условиям (23) и (24), будем искать методом Фурье (называемым также методом разделения переменных). Метод Фурье состоит в том, что частные решения ищутся в виде произведения двух функций, одна из которых зависит только от x, а другая только от t. То есть мы ищем решения уравнения (21), которые имеют специальный вид: u(x, t) = X(x)T(t), (25) где X дважды непрерывно дифференцируемая функция от x на [, l], а T дважды непрерывно дифференцируемая функция от t, t >. Substituindo (25) em (21), obtemos: X T = α 2 X T, (26) ou T (t) α 2 T(t) = X (x) X(x). (27) Diz-se que houve uma separação de variáveis. Como x e t não dependem um do outro, o lado esquerdo em (27) não depende de x, mas o lado direito não depende de t, e o valor total dessas razões é 62

63 deve ser constante, o que denotamos por λ: T (t) α 2 T(t) = X (x) X(x) = λ. Daí obtemos duas equações diferenciais ordinárias: X (x) λx(x) =, (28) T (t) α 2 λt(t) =. (29) Neste caso, as condições de contorno (22) assumem a forma X()T(t) = e X(l)T(t) =. Como eles devem ser cumpridos para todo t, t >, então X() = X(l) =. (3) Vamos encontrar soluções para a equação (28) satisfazendo as condições de contorno (3). Vamos considerar três casos. Caso 1: λ >. Denote λ = β 2. A equação (28) assume a forma X (x) β 2 X(x) =. Sua equação característica k 2 β 2 = tem raízes k = ±β. Portanto, a solução geral da Eq. (28) tem a forma X(x) = C e βx + De βx. Devemos escolher as constantes C e D de modo que as condições de contorno (3) sejam atendidas, ou seja, X() = C + D =, X(l) = C e βl + De βl =. Desde β, então este sistema de equações tem uma única solução C = D =. Daí X(x) e 63

64 u(x, t). Assim, no caso 1 obtivemos uma solução trivial, que não iremos considerar mais adiante. Caso 2: λ =. Então a equação (28) assume a forma X (x) = e sua solução é obviamente dada pela fórmula: X(x) = C x+d. Substituindo esta solução nas condições de contorno (3), obtemos X() = D = e X(l) = Cl =, portanto C = D =. Daí X(x) e u(x, t), e novamente temos uma solução trivial. Caso 3: λ<. Обозначим λ = β 2. Уравнение (28) принимает вид: X (x)+β 2 X(x) =. Его характеристическое уравнение имеет вид k 2 + β 2 =, а k = ±βi являются его корнями. Следовательно, общее решение уравнения (28) в этом случае имеет вид X(x) = C sin βx + D cosβx. В силу граничных условий (3) имеем X() = D =, X(l) = C sin βl =. Поскольку мы ищем нетривиальные решения (т. е. такие, когда C и D не равны нулю одновременно), то из последнего равенства находим sin βl =, т. е. βl = nπ, n = ±1, ±2,..., n не равно нулю, так как сейчас мы рассматриваем случай 3, в котором β. Итак, если β = nπ (nπ) 2, l, т. е. λ = то существуют l решения X n (x) = C n sin πnx, (31) l C n произвольные постоянные, уравнения (28), не равные тождественно нулю. 64

65 A seguir, atribuiremos a n apenas valores positivos n = 1, 2,..., pois para n negativo obteremos soluções da mesma forma (nπ). Os valores λ n = são chamados autovalores, e as funções X n (x) = C n sen πnx autofunções da equação diferencial (28) com condições de contorno (3). Agora vamos resolver a equação (29). Para ele, a equação característica tem a forma k 2 α 2 λ =. (32) l 2 Como descobrimos acima que soluções não triviais X(x) da Eq. (28) existem apenas para λ negativo igual a λ = n2 π 2, são esses λ que consideraremos a seguir. As raízes da equação (32) são k = ±iα λ, e as soluções da equação (29) têm a forma: T n (t) = A n sen πnαt + B n cos πnαt, (33) l l onde A n e B n são constantes arbitrárias. Substituindo as fórmulas (31) e (33) em (25), encontramos soluções particulares da equação (21) que satisfazem as condições de contorno (22): (u n (x, t) = B n cos πnαt + A n sen πnαt) C n pecado pnx. l l l Colocando o fator C n entre colchetes e introduzindo a notação C n A n = b n e B n C n = a n, escrevemos u n (X, T) como (u n (x, t) = a n cos πnαt + b n sen πnαt ) pecado pnx. (34) l l l 65

66 As vibrações da corda correspondentes às soluções u n (x, t) são chamadas de vibrações naturais da corda. Como a equação (21) e as condições de contorno (22) são lineares e homogêneas, então uma combinação linear de soluções (34) (u(x, t) = a n cos πnαt + b n sen πnαt) sen πnx (35) l l l será um solução da equação (21 ) satisfazendo as condições de contorno (22) com uma escolha especial dos coeficientes a n e b n, o que garante a convergência uniforme da série. Agora escolhemos os coeficientes a n e b n da solução (35) de modo que ela satisfaça não apenas as condições de contorno, mas também as condições iniciais (23) e (24), onde f(x), g(x) são funções dadas ( além disso, f() = f(l) = g() = g(l) =). Assumimos que as funções f(x) eg(x) satisfazem as condições de expansão de Fourier. Substituindo o valor t = em (35), obtemos u(x,) = a n sen πnx l = f(x). Diferenciando a série (35) em relação a t e substituindo t =, obtemos u t (x,) = πnα b n sin πnx l l = g(x), e esta é a expansão das funções f(x) e g(x) em série de Fourier. Portanto, a n = 2 l l f(x) sen πnx l dx, b n = 2 l g(x) sen πnx dx. πnα l (36) 66

67 Substituindo as expressões dos coeficientes a n e b n em séries (35), obtemos uma solução para a equação (21) que satisfaz as condições de contorno (22) e iniciais (23) e (24). Assim, resolvemos o problema das pequenas vibrações transversais livres de uma corda. Vamos esclarecer o significado físico das autofunções u n (x, t) do problema das vibrações livres de uma corda, definidas pela fórmula (34). Vamos reescrever como onde u n (x, t) = α n cos πnα l α n = a 2 n + b2 n, (t + δ n) sin πnx, (37) l πnα δ n = arctg b n. l a n A fórmula (37) mostra que todos os pontos da corda realizam oscilações harmônicas com a mesma frequência ω n = πnα e fase πnα δ n. A amplitude de oscilação depende de l l a abcissa x do ponto da corda e é igual a α n sen πnx. Com tal oscilação, todos os pontos da corda atingem simultaneamente seu l desvio máximo em uma direção ou outra e simultaneamente passam pela posição de equilíbrio. Tais oscilações são chamadas de ondas estacionárias. Uma onda estacionária terá n + 1 pontos fixos dados pelas raízes da equação sen πnx = no intervalo [, l]. Os pontos fixos são chamados de nós da onda estacionária. No meio entre os nós - l mi estão os pontos em que os desvios atingem um máximo; tais pontos são chamados de antinós. Cada corda pode ter suas próprias oscilações de frequências estritamente definidas ω n = πnα, n = 1, 2,.... Essas frequências são chamadas de frequências naturais da corda. O l mais baixo que uma corda pode produzir é determinado por ela mesma 67

68 baixa frequência natural ω 1 = π T e é chamado de tom fundamental da corda. Os tons restantes correspondentes às frequências l ρ ω n, n = 2, 3,..., são chamados harmônicos ou harmônicos. Para maior clareza, representaremos os perfis típicos de uma corda emitindo o tom fundamental (Fig. 33), o primeiro harmônico (Fig. 34) e o segundo harmônico (Fig. 35). Arroz. Fig. 33. Perfil da corda que emite o tom fundamental. Fig. 34. Perfil de uma corda emitindo o primeiro harmônico. Fig. 35. Perfil de uma corda emitindo um segundo harmônico Se a corda executa vibrações livres determinadas pelas condições iniciais, então a função u(x, t) é representada, como pode ser visto na fórmula (35), como uma soma de harmônicos individuais. Assim oscilação arbitrária 68

A 69ª corda é uma superposição de ondas estacionárias. Neste caso, a natureza do som da corda (tom, força do som, timbre) dependerá da razão entre as amplitudes dos harmônicos individuais Força, tom e timbre do som Uma corda vibrante excita as vibrações do ar percebidas pelo ser humano ouvido como um som emitido por uma corda. A força do som é caracterizada pela energia ou amplitude das vibrações: quanto maior a energia, maior a força do som. O tom de um som é determinado por sua frequência ou período de oscilação: quanto mais alta a frequência, mais alto o som. O timbre do som é determinado pela presença de harmônicos, a distribuição de energia sobre harmônicos, ou seja, o método de excitação das oscilações. As amplitudes dos harmônicos são, em geral, menores que a amplitude do fundamental, e as fases dos harmônicos podem ser arbitrárias. Nosso ouvido não é sensível à fase das oscilações. Compare, por exemplo, as duas curvas da Fig. 36, emprestado de . Trata-se de uma gravação de som com o mesmo tom fundamental, extraído do clarinete (a) e do piano (b). Ambos os sons não são simples oscilações sinusoidais. A frequência fundamental do som em ambos os casos é a mesma e isso cria o mesmo tom. Mas os padrões de curva são diferentes porque harmônicos diferentes são sobrepostos ao tom fundamental. De certo modo, esses desenhos mostram o que é o timbre. 69

Equações do tipo hiperbólica. Vibrações de uma corda infinita e semi-infinita. Método de Fourier Método de Fourier Ondas estacionárias 4 Aula 4.1 Equações do tipo hiperbólicas. Flutuações de infinito e semi-infinito

UNIVERSIDADE TÉCNICA DO ESTADO DE MOSCOVO DE AVIAÇÃO CIVIL V.M. Lyubimov, E.A. Zhukova, V.A. Ukhova, Yu.A. Shurinov

MINISTÉRIO DA EDUCAÇÃO E CIÊNCIA DA RÚSSIA Instituição educacional orçamentária do estado federal de educação profissional superior MATI Universidade Tecnológica do Estado Russo em homenagem a K. E. Tsiolkovsky

Ministério da Educação da República da Bielorrússia Vitebsk State Technological University Topic. "Rows" Departamento de Matemática Teórica e Aplicada. desenvolvido pela Assoc. E.B. Dunina. Principal

Agência Federal de Educação Instituição Estadual Federal de Educação Profissional Superior UNIVERSIDADE FEDERAL DO SUL R. M. Gavrilova, G. S. Kostetskaya Metódica

Tópico Série de Fourier Aula prática Série de Fourier em sistemas ortogonais de funções Espaço de funções contínuas por partes Série de Fourier generalizada 3 Desigualdade de Bessel e convergência de séries de Fourier Espaço

TEORIA DAS SÉRIES A teoria das séries é o componente mais importante da análise matemática e encontra aplicações tanto teóricas quanto práticas. Distinguir entre séries numéricas e funcionais.

SUMÁRIO Série de Fourier 4 O conceito de função periódica 4 Polinômio trigonométrico 6 3 Sistemas ortogonais de funções 4 Série de Fourier trigonométrica 3 5 Série de Fourier para funções pares e ímpares 6 6 Decomposição

Agência Federal de Educação Universidade Estadual de Geodésia e Cartografia de Moscou (MIIGAiK) INSTRUÇÕES METODOLÓGICAS E TAREFAS PARA TRABALHO INDEPENDENTE no curso MATEMÁTICA SUPERIOR

Aula 4. Análise harmônica. Série de Fourier Funções periódicas. Análise harmônica Em ciência e tecnologia, muitas vezes é preciso lidar com fenômenos periódicos, ou seja, aqueles que se repetem

TÓPICO V SÉRIE DE FOURIER AULA 6 Expansão de uma função periódica em uma série de Fourier Muitos processos que ocorrem na natureza e na tecnologia têm a propriedade de se repetir em determinados intervalos Tais processos

INSTRUÇÕES METODOLÓGICAS PARA TAREFAS DE CÁLCULO NO CURSO DE MATEMÁTICA SUPERIOR "SÉRIE DE EQUAÇÕES DIFERENCIAIS ORDINÁRIAS INTEGRAIS DUPLOS" PARTE III SÉRIE TEMÁTICA Conteúdos Série Séries numéricas Convergência e divergência

6 Série de Fourier 6 Sistemas ortogonais de funções Série de Fourier em função de um sistema ortogonal de funções As funções ϕ () e ψ (), definidas e integráveis ​​no segmento [, ], dizem-se ortogonais neste segmento se

INTEGRAL DEFINIDA. Somas Integrais e Integrais Definidas Seja uma função y = f () definida no segmento [, b ], onde< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных

5 Séries de potências 5 Séries de potências: definição, domínio de convergência Séries de funções na forma (a + a) + a () + K + a () + K a) (, (5) números são chamados de séries de potências Números

FACULDADE DE MATEMÁTICA APLICADA E CIÊNCIAS DA INFORMAÇÃO DA UNIVERSIDADE ESTADUAL DA BELARUSIA Auxiliar de ensino para alunos da Faculdade de Matemática Aplicada e Informática

Vejamos alguns exemplos. Exemplo. Vamos encontrar a soma de uma progressão geométrica infinita A fórmula do termo comum desta série é a+aq+...+aq n +... (a). a n = aq n. Vamos calcular suas somas parciais. Se q =, então

Tarefa 1.1. Encontre soluções y = y(x) da equação diferencial que não sejam identicamente zero na área indicada e satisfaçam as condições de contorno dadas (o problema de Sturm-Liouville) Solução: Considere

Análise matemática Tópico: Integral definida Integrais impróprios Palestrante Pakhomova E.G. 2017 CAPÍTULO II. Integral definida e suas aplicações 1. Integral definida e suas propriedades 1. Tarefas,

Aula 8 4 Problema de Sturm-Liouville

Explicações ao texto: o sinal é lido como "equivalente" e significa que as equações à direita do sinal e à esquerda do sinal têm o mesmo conjunto de soluções, o sinal IR denota o conjunto dos números reais, o sinal EM

82 4. Seção 4. Séries funcionais e de potências 4.2. Aula 3 4.2. Lição 3 4.2.. Expansão de Taylor de uma função DEFINIÇÃO 4.2.. Seja a função y = f(x) infinitamente diferenciável em alguma vizinhança

MINISTÉRIO DA EDUCAÇÃO E CIÊNCIA DA RÚSSIA ORÇAMENTO DO ESTADO FEDERAL INSTITUIÇÃO DE ENSINO SUPERIOR PROFISSIONAL "UNIVERSIDADE TÉCNICA DO ESTADO DE SAMARA" Departamento de Matemática Aplicada

Agência Federal de Transporte Ferroviário Ural State University of Railway Transport Department "Matemática Superior e Aplicada" N. P. Chuev Elementos da Análise Harmônica Metódica

Aula 3 Séries de Taylor e Maclaurin Aplicação de séries de potências Expansão de funções em séries de potências Séries de Taylor e Maclaurin Para aplicações, é importante poder expandir uma dada função em séries de potências, essas funções

S A Lavrenchenko wwwwrckoru Palestra Transformação de Fourier Conceito de transformação integral O método de transformações integrais é um dos métodos poderosos da física matemática e é uma solução poderosa

Integrabilidade de uma função (de acordo com Riemann) e uma integral definida Exemplos de resolução de problemas 1. A função constante f(x) = C é integrável em , pois para quaisquer partições e qualquer escolha de pontos ξ i a integral

Eu claro, tarefa. Prove que a função de Riemann, se 0, m m R(), se, m, m 0, e a fração é irredutível, 0, se irracional, é descontínua em todo ponto racional e contínua em todo ponto irracional. Solução.

1 2 Índice 1 Série de Fourier 5 1.1 Série trigonométrica de Fourier ............... 5 1.2 Apenas seno e cos .............. ............ 7 1.3 Série de Fourier na forma complexa............. 11 1.4 f(x) = c k?......... ......

EQUAÇÕES DA FÍSICA MATEMÁTICA 1. Equações diferenciais parciais

Aula 4. Equações de onda 1. Derivação da equação das vibrações das cordas 2. Equação das vibrações longitudinais de uma haste 3. Condições iniciais, condições de contorno 4. Enunciado do problema 1. Derivação da equação das vibrações das cordas

1. Eletrostática 1 1. Eletrostática Lição 6 Separação de variáveis ​​em coordenadas cartesianas 1.1. (Problema 1.49) O plano z = é carregado com densidade σ (x, y) = σ sin (αx) sin (βy), onde σ, α, β são constantes.

Módulo Tópico Sequências e séries de funções Propriedades de convergência uniforme de sequências e séries Séries de potências Aula Definições de sequências e séries de funções Uniformemente

Equações do tipo parabólica. Método de separação de variáveis ​​Problema de valor de contorno homogêneo Função fonte Equação de calor não homogêneo 7 Aula 7.1 Equações do tipo parabólico. Método de separação

Aula Séries numéricas Sinais de convergência Séries numéricas Sinais de convergência Uma expressão infinita de uma sequência numérica + + + +, composta de membros de uma sequência infinita, é chamada de série numérica

35 7 Trigonométrica Série de Fourier Série de Fourier para funções periódicas com período T. Seja f(x) uma função periódica contínua por partes com período T. Considere o sistema trigonométrico básico

Faculdade de Metalurgia Departamento de Matemática Superior

Departamento de Matemática e Informática Elementos de Matemática Superior Complexo pedagógico e metodológico para alunos do ensino secundário profissional que estudam com recurso a tecnologias a distância Módulo Cálculo diferencial Compilado por:

9. Antiderivada e integral indefinida 9. Seja dada a função f() no intervalo I R. A função F () é chamada de função antiderivada f() no intervalo I, se F () = f() para qualquer I, e a antiderivada

DIFERENCIAÇÃO DE FUNÇÕES DE UMA VARIÁVEL O conceito de derivada, seu significado geométrico e físico Problemas que conduzem ao conceito de derivada Definição da tangente S à reta y f (x) no ponto A x ; f(

Equações do tipo hiperbólica. Vibrações de uma corda infinita e semi-infinita. Método de d'Alembert String infinita. Fórmula de d'Alembert Corda semi-infinita 3 Aula 3.1 Equações do tipo hiperbólica.

Título Introdução. Conceitos básicos.... 4 1. Equações integrais de Volterra... 5 Opções de trabalho de casa.... 8 2. Resolvente da equação integral de Volterra. 10 Opções de lição de casa.... 11

LINHAS. Número de linhas. Definições básicas Seja dada uma sequência infinita de números A expressão (soma infinita) a, a 2,..., a n,... a i = a + a 2 + + a n +... () i= é chamada de a série numérica. Números

8. Série de potências 8.. Uma série funcional na forma c n (z) n, (8.) n= onde c n é uma sequência numérica, R é um número fixo e z R é chamado de série de potências com coeficientes c n . Ao mudar as variáveis

~ ~ Integrais indefinidas e definidas O conceito de antiderivada e integral indefinida. Definição: Uma função F é chamada antiderivada em relação a uma função f se essas funções estiverem relacionadas da seguinte forma

3724 SÉRIES DE INTEGRAIS MÚLTIPLOS E CURVILÍNEOS 1 PROGRAMA DE TRABALHO DAS SEÇÕES "SÉRIES DE INTEGRAIS MÚLTIPLOS E CURVILÍNEOS" 11 Série numérica O conceito de série numérica Propriedades da série numérica Um critério necessário para a convergência

COMER. ORE ANÁLISE MATEMÁTICA. SÉRIE NUMÉRICA E FUNCIONAL NOVOSIBIRSK 200 2 MINISTÉRIO DA EDUCAÇÃO E CIÊNCIA DA RUSSA SEI HPE "UNIVERSIDADE PEDAGÓGICA DO ESTADO DE NOVOSIBIRSK" E.M. Rudoy ANÁLISE MATEMÁTICA.

PALESTRA N 7 .Poder

EQUAÇÕES QUADRÁTICAS

SEÇÃO DE TAREFAS COM PARÂMETROS Comentário Tarefas com parâmetros são tradicionalmente tarefas complexas na estrutura USE, exigindo do candidato não apenas o domínio de todos os métodos e técnicas de resolução de diversos

Cálculo diferencial Introdução à análise matemática Limite de sequência e função. Divulgação de incertezas internas. Função derivada. Regras de diferenciação. Aplicação da derivada

Série de Fourier Sistemas ortogonais de funções Do ponto de vista da álgebra, a igualdade onde são funções de uma determinada classe e são coeficientes de R ou C simplesmente significa que o vetor é uma combinação linear dos vetores B

1. Integral definido 1.1. Seja f uma função limitada definida no segmento [, b] R. Uma partição do segmento [, b] é um conjunto de pontos τ = (x, x 1,..., x n 1, x n ) [, b ] tal que = x< x 1 < < x n 1

Ch Série de potências a a a Uma série da forma a a a a a () é chamada de série de potências, onde, a, são constantes, chamadas de coeficientes da série. Às vezes, uma série de potências de uma forma mais geral é considerada: a a (a) a ( a) a (a) (), onde

segue:

1) desenhe um gráfico f(x) em um intervalo de pelo menos dois períodos, para mostrar que a função dada é periódica;

2) desenhe um gráfico S(x) da mesma forma, para que se possa ver em que pontos f(x)¹S(x);

3) calcule os coeficientes de Fourier e escreva a série de Fourier.

Tarefas

№1. Expandir em uma série de Fourier

Solução. notar que f(x) dado no intervalo de comprimento T=4. Porque f(x)é considerado periódico, então é esse número que é seu período, então - l = 2.

1) Gráfico f(x):

2) Gráfico S(x):

As setas no final das linhas indicam que a função não assume no final do intervalo o valor determinado a partir da expressão dada no intervalo. Ao comparar gráficos f(x) E S(x)é claramente visto que nos pontos de descontinuidade f(x)¹S(x).

3) Calcule os coeficientes de Fourier. Isso pode ser feito usando as fórmulas (3*): ; ; . Exatamente: ; Então,

Decomposição f(x) em uma série de Fourier tem a forma:

Observações . 1) Ao integrar em [-1;3] esta seção foi dividida em E , porque nesses segmentos f(x) definido para valores diferentes.

2) Ao calcular os coeficientes, integrais foram usados: e , onde a = const.

№2 . Expandir em uma série de Fourier

Solução. Aqui T=2, l = 1.

A série de Fourier tem a forma: , onde ; ; , porque l = 1.

1) Gráfico f(x):

2) Gráfico S(x):

№3. Expandir em uma série de Fourier em termos de senos

Solução. Observe que apenas as funções ímpares são expandidas na série de Fourier em termos de senos. Porque f(x) definido apenas para x > 0, xí(0;2)É(2;3), então isso significa que no intervalo simétrico (-3;-2)È(-2;0) f(x) deve ser mantido de tal forma que a igualdade f(-x) = -f(x). Portanto, a duração do intervalo em que f(x) dada como uma função ímpar, é igual a 6. Portanto T = 6, l = 3. Série de Fourier para f(x) tem a forma: , onde , n = 1, 2, 3, (de acordo com as fórmulas (5")).

1) Gráfico f(x).

Para desenhar um gráfico f(x) como uma função ímpar, primeiro desenhamos um gráfico em (0;2)È(2;3), e aproveite o fato de que o gráfico de uma função ímpar é simétrico em relação à origem. A partir dessas considerações, obtemos o gráfico f(x) sobre (-3;-2)È(-2;0). Então continuamos f(x) T=6.

2) Gráfico S(x).

Agendar S(x) diferente do gráfico f(x) nos pontos de quebra da função f(x). Por exemplo, em t. x = 2f(x) não definido, mas S(x) tem em x=2 um valor igual à metade da soma dos limites laterais da função f(x), exatamente: , Onde , .

Então a decomposição f(x) em uma série de Fourier tem a forma: .

№4 . Expanda em uma série de Fourier em cossenos.

Solução. Observe que apenas funções pares podem ser expandidas na série de Fourier em cossenos. Porque f(x) definido apenas para x>0, xí(0;2)É(2;3], então isso significa que no intervalo simétrico [-3;-2)È(-2;0) f(x) precisamos continuar de tal forma que a igualdade seja válida: f(-x) = f(x). Portanto, a duração do intervalo em que f(x) dado como uma função par é igual a 6, então T = 6, l = 3. A série de Fourier neste caso tem a forma:

Onde ; ; n=1,2,...(de acordo com as fórmulas (4")).

1) Gráfico f(x).

Para desenhar um gráfico f(x) como uma função par, primeiro desenhamos um gráfico f(x) sobre (0;2)È(2;3], e aproveite o fato de que o gráfico de uma função par é simétrico em relação ao eixo y. A partir dessas considerações, obtemos o gráfico f(x) sobre [-3;-2)È(-2;0). Então continuamos f(x) em toda a reta numérica como uma função periódica com período T=6.

aqui está o gráfico f(x) desenhados em dois períodos completos da função.

2) Gráfico S(x).

Agendar S(x) diferente do gráfico f(x) nos pontos de quebra da função f(x). Por exemplo, em t. x = 0 f(x) não definido, mas S(x) tem o significado: , então o gráfico S(x) não é interrompido em x=0, ao contrário do gráfico f(x).

Decomposição f(x) em uma série de Fourier em cossenos tem a forma: .

№5. Expandir em uma série de Fourier f(x) = |x|, xí(-2;2)..

Solução. Por condição, f(x)é uma função par em (-2;2) ; aqueles. sua série de Fourier contém apenas cossenos, enquanto T = 4, l = 2, ,

Onde ; ; n = 1, 2,

1) Gráfico f(x):

2) Gráfico S(x):

3), porque |x| = x Para x > 0.; .

Então a decomposição f(x) em uma série de Fourier tem a forma: . Observe que ao integrar expressões ou , a fórmula de integração por partes é usada: , onde u=x; dv = cos(ax)dx ou dv = sen(ax)dx.

№6. Expanda a função em uma série de Fourier: a) no intervalo (-?,?); b) no intervalo (0, 2?); c) no intervalo (0, ?) em uma série de senos.

Solução. a) Gráfico de uma função com 2? - a continuação periódica tem a forma

A função satisfaz as condições do teorema de Dirichlet e, portanto, pode ser expandida em uma série de Fourier.

Vamos calcular os coeficientes de Fourier. Como a função é par, então bn = 0 (n = 0, 1, 2,…) e (n = 0, 1, 2,…).

Para calcular essa integral, utiliza-se a fórmula de integração por partes em uma integral definida. Nós temos

A série de Fourier desta função tem a forma . Em virtude do teste de Dirichlet, esta série representa a função x2 no intervalo (-?,?).

b) O intervalo (0, 2?) não é simétrico em relação à origem e seu comprimento é 2 eu= 2?. Calculamos os coeficientes de Fourier usando as fórmulas:

Portanto, a série de Fourier tem a forma . Em virtude do teorema de Dirichlet, a série converge para uma função geradora nos pontos x?(0,2?), e nos pontos 0 e 2? dar valor. O gráfico da soma da série se parece com

c) A função expandida em uma série em termos de senos deve ser ímpar. Portanto, estendemos a função dada x2 em (-π,π) de forma ímpar, ou seja, considere a função. Para esta função f(x) temos an = 0 (n = 0, 1, 2,…) e

A expansão desejada tem a forma .

O gráfico da soma da série se parece com

Observe que nos pontos x = (-π, π) a série de Fourier converge para zero.

№7 Expanda em uma série de Fourier uma função dada graficamente:

Solução . Obtemos uma expressão explícita para f(x). O gráfico da função é uma reta, usamos a equação de uma reta na forma. Como pode ser visto no desenho, ou seja, f(x) = x - 1 (-1< x < 1) и период Т = 2.

Esta função satisfaz as condições do teste de Dirichlet, então ela se expande em uma série de Fourier. Vamos calcular os coeficientes de Fourier ( eu = 1):

; (n = 1, 2,…);

A série de Fourier para a função f(x) tem a forma

Representa a função f(x) em -1< x < 1, а в точках х0 = -1 и х0 = 1 ряд сходится к -1.

№8. Expanda a função em uma série trigonométrica de Fourier em um segmento e indique a função para a qual a série resultante converge.

Solução. Desenhe um gráfico de uma função, continuando-o periodicamente com um período ou em todo o eixo. A função continuada tem um período.

Verifique as condições de condições suficientes para a convergência da série de Fourier (Dini-Lipschitz, Jordan, Dirichlet).

A função é monotônica por partes no segmento: aumenta continuamente. Em pontos, a função tem descontinuidades do primeiro tipo.

Descubra se uma função é par ou ímpar: A função não é nem par nem ímpar.

a) se a função estiver definida para

b) se a função estiver configurada para

Componha a série de Fourier da função: .

Especifique a função para a qual esta série irá convergir, usando critérios de convergência pontual: De acordo com o critério de Dirichlet, a série de Fourier da função converge para a soma:

№9. Expanda a função em uma série de Fourier em termos de senos e use essa expansão para encontrar a soma da série de números.

Solução. Continue a função de maneira par (ímpar) em (- p,0) ou (- eu,0), e então periodicamente com período 2 p ou 2 eu continuar a função para todo o eixo.

Continuamos a função de forma ímpar em , e então periodicamente, com um ponto , continuamos em todo o eixo.

Desenhe um gráfico de continuação periódica. Teremos uma função da forma:

Verifique as condições de condições suficientes para a convergência da série de Fourier (Dini-Lipitz, Jordan, Dirichlet).

A função é constante por partes no intervalo: é igual a -1 em e 1 em . Em pontos, a função tem descontinuidades do primeiro tipo.

Calcule os coeficientes de Fourier:

Seus coeficientes de Fourier são calculados pelas fórmulas:

Componha a série de Fourier da função. .

Especifique a função para a qual esta série irá convergir, usando critérios de convergência pontual.

De acordo com o teste de Dirichlet, a série de Fourier da função converge para a soma:

Portanto, quando

Substituindo os valores, indique a soma da série numérica dada.

Assumindo na decomposição resultante , encontramos ,

de onde, desde , .

№10. Escreva a igualdade de Parseval para a função e, com base nessa igualdade, encontre a soma da série numérica.

Solução. Determine se a função dada é uma função quadrada integrável em .

A função é contínua e, portanto, integrável em . Pela mesma razão, seu quadrado é integrável em .

Calcule os coeficientes de Fourier usando as fórmulas:

Por ser uma função ímpar, seus coeficientes de Fourier são calculados pelas fórmulas:

Calcular integral.

Escreva a fórmula de Parseval:

Assim, a fórmula de Parseval tem a forma

Tendo realizado, se necessário, operações aritméticas nos lados direito e esquerdo, obtenha a soma da série numérica dada.

Dividindo ambas as partes da igualdade resultante por 144, encontramos: .

№11. Encontre a Integral de Fourier de uma Função

e construa seu gráfico.

Solução. Plote a função.

Verifique o cumprimento das condições de condições suficientes para a convergência da integral de Fourier (Dini, Dirichlet-Jordan ou consequências delas).

A função é absolutamente integrável no intervalo, contínua para e , e tem uma descontinuidade do primeiro tipo em um ponto. Além disso, para e a função tem uma derivada finita, e em zero existem derivadas direita e esquerda finitas. Descubra se a função é par ou ímpar. A função não é par nem ímpar. ; .

Então, ou,