Ponto especial. Pontos singulares isolados Um exemplo de um ponto singular isolado

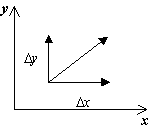
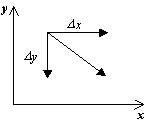
A série de Taylor serve como uma ferramenta eficaz para estudar funções analíticas no círculo zol Para estudar funções analíticas em uma região anular, verifica-se que é possível construir expansões em potências positivas e negativas (z - zq) do forma que generaliza as expansões de Taylor. A série (1), entendida como a soma de duas séries, é chamada de série de Laurent. É claro que a região de convergência da série (1) é a parte comum das regiões de convergência de cada uma das séries (2). Vamos encontrá-la. A área de convergência da primeira série é um círculo cujo raio é determinado pela fórmula de Cauchy-Hadamard Dentro do círculo de convergência, a série (3) converge para uma função analítica, e em qualquer círculo de menor raio, converge absolutamente e uniformemente. A segunda série é uma série de potências em relação à variável. A série (5) converge dentro de seu círculo de convergência para a função analítica da variável complexa m-*oo, e em qualquer círculo de menor raio ela converge absoluta e uniformemente, o que significa que a região de convergência da série (4) é a aparência do círculo - Se então existe uma região comum de convergência das séries (3) e (4) - um anel circular no qual a série (1) converge para uma função analítica. Além disso, em qualquer anel, converge absoluta e uniformemente. Exemplo 1. Determinar a região de convergência da série de rad Laurent Pontos singulares isolados e sua classificação (z), que é univalorada e apolítica em um anel circular, podem ser representados neste anel como a soma de uma série convergente cujos coeficientes Cn são unicamente determinados e calculados pelas fórmulas onde 7p é um círculo de raio m Fixemos um ponto arbitrário z dentro do anel R Construímos círculos com centros no ponto r0 cujos raios satisfazem as desigualdades e consideramos um novo anel.De acordo com o teorema da integral de Cauchy para um domínio multiplamente conexo, temos Transformemos cada uma das integrais na soma (8) separadamente. Para todos os pontos £ ao longo do círculo 7d*, a relação de a soma de uma série uniformemente convergente 1 1 é satisfeita. Portanto, a fração ^ pode ser representada em vi- /" / Para todos os pontos £ no círculo ir> a relação é satisfeita Portanto, a fração ^ pode ser representada como a soma de uma série uniformemente convergente nas fórmulas (10) e (12) são funções analíticas em um anel circular. Portanto, pelo teorema de Cauchy, os valores das integrais correspondentes não mudam se os círculos 7/r e 7r/ forem substituídos por qualquer círculo. Isso nos permite combinar as fórmulas (10) e (12). Substituindo as integrais do lado direito da fórmula (8) por suas expressões (9) e (11), respectivamente, obtemos a expansão desejada. Como z é um valor arbitrário ponto do anel, segue-se que a série (14) converge para a função f(z) em todos os pontos deste anel, e em qualquer anel a série converge para esta função absoluta e uniformemente. Provemos agora que a decomposição da forma (6) é única. Suponha que ocorra mais uma decomposição, então, em todo o interior do anel R, temos Na circunferência, as séries (15) convergem uniformemente. Multiplique ambos os lados da igualdade (onde m é um número inteiro fixo e integre ambas as séries termo a termo. Como resultado, obtemos no lado esquerdo e no lado direito - Csh. Assim, (4, \u003d St. Como m é um número arbitrário, a última série de igualdade (6), cujos coeficientes são calculados pelas fórmulas (7), é chamada de série de Laurent da função f(z) no anel 7) para os coeficientes do As séries de Laurent raramente são usadas na prática, porque, via de regra, requerem cálculos complicados. Normalmente, se possível, são usadas expansões de Taylor prontas de funções elementares. Com base na singularidade da expansão, qualquer método legítimo leva ao mesmo resultado. Exemplo 2 Considere as expansões em série de Laurent das funções de diferentes domínios, assumindo que Fuiscija /(z) tem dois pontos singulares: Portanto, existem três domínios de anéis e, centrado no ponto r = 0. em cada um dos quais a função f(r) é analítica: a) o círculo é o exterior do círculo (Fig. 27). Vamos encontrar as expansões de Laurent da função /(z) em cada uma dessas regiões. Representamos /(z) como uma soma de frações elementares a) Relação da Transformada do Círculo (16) como segue Usando a fórmula para a soma dos termos de uma progressão geométrica, obtemos b) O anel para a função -z permanece convergente neste anel, pois a Série (19) para a função j^j para |z| > 1 diverge. Portanto, transformamos a função /(z) da seguinte forma: aplicando a fórmula (19) novamente, obtemos que Esta série converge para. Substituindo as expansões (18) e (21) na relação (20), obtemos c) A exterioridade do círculo para a função -z com |z| > 2 diverge, e série (21) para a função Vamos representar a função /(z) da seguinte forma: /<*> Usando as fórmulas (18) e (19), obtemos OR 1 Este exemplo mostra que para a mesma função f(z) a expansão de Laurent, de modo geral, tem uma forma diferente para diferentes anéis. Exemplo 3. Encontre a decomposição da série de 8 Laurent da função Série de Laurent Pontos singulares isolados e sua classificação na região anular A Usamos a representação da função f (z) da seguinte forma: e transformamos o segundo termo Usando o fórmula para a soma dos termos de uma progressão geométrica, obtemos Substituindo as expressões encontradas na fórmula (22), temos o Exemplo 4. Expandir a função em uma série de Laurent na vizinhança de fino zq = 0. Para qualquer complexo , temos Let Esta expansão é válida para qualquer ponto z Ф 0. Neste caso, a região anular é todo o plano complexo com um ponto z jogado fora - 0. Esta região pode ser definida pela seguinte relação: Esta função é analítica na região Das fórmulas (13) para os coeficientes da série de Laurent, pelo mesmo raciocínio do parágrafo anterior, obtém-se as desigualdades de Kouiw. se a função f(z) é limitada por um círculo, onde M é uma constante), então pontos singulares isolados Um ponto zo é chamado de ponto singular isolado da função f(z) se existe uma vizinhança anular do ponto ( esse conjunto às vezes também é chamado de vizinhança perfurada do ponto 2o), em que a função f(z) é de valor único e analítica. No próprio ponto zo, a função não é definida ou não é de valor único e analítica. Distinguem-se três tipos de pontos singulares em função do comportamento da função /(z) ao aproximar-se do ponto zo. Um ponto singular isolado é chamado: 1) removível se existe um finito 2) pmusach se 3) um ponto essencialmente singular se a função f(z) não tem limite para Teorema 16. Um ponto singular isolado z0 de uma função f(z) é um ponto singular removível se e somente se a expansão de Laurent da função f(z) em uma vizinhança do ponto zo não contém uma parte principal, ou seja, tem a forma Let zo - ponto singular removível. Então existe um finito e, portanto, a função f(z) é limitada em uma vizinhança pró-lógica do ponto r. Definimos Em virtude das desigualdades de Cauchy Como é possível escolher p como arbitrariamente pequeno, então todos os coeficientes em negativo potências (z - 20) são iguais a zero: Inversamente, deixe o Laurent a expansão da função /(r) em uma vizinhança do ponto zq conter apenas a parte correta, ou seja, tem a forma (23) e, portanto , é Taylor. É fácil ver que para z -* z0 a função /(r) tem um valor limite: Teorema 17. Um ponto singular isolado zq da função f(z) é removível se e somente se a função J(z) é limitado em alguma vizinhança perfurada do ponto zq, Zgmechai não. Seja r0 um ponto singular removível de f(r). Assumindo obtemos que a função f(r) é analítica em algum círculo centrado no ponto th. Isso define o nome do ponto - descartável. Teorema 18. Um ponto singular isolado zq de uma função f(z) é um pólo se e somente se a parte principal da expansão de Laurent da função f(z) em uma vizinhança do ponto contém um número finito (e positivo) de termos diferentes de zero, ou seja, tem a forma 4 Seja z0 um pólo. Desde então existe uma vizinhança pontuada do ponto z0 na qual a função f(z) é analítica e diferente de zero. Em seguida, uma função analítica é definida nesta vizinhança e, portanto, o ponto zq é um ponto singular removível (zero) da função ou onde h(z) é uma função analítica, h(z0) ∩ 0. é analítica em uma vizinhança do ponto zq, e portanto, de onde obtemos que Vamos agora assumir que a função f(z) tem uma decomposição da forma (24) em uma vizinhança pontuada do ponto zo. Isso significa que nessa vizinhança a função f(z) é analítica junto com a função. Para a função g(z), a expansão é válida a partir da qual fica claro que zq é um ponto singular removível da função g(z) e existe Então a função tende a 0 - o pólo da função Há mais um simples facto. O ponto Zq é um pólo da função f(z) se e somente se a função g(z) = y pode ser estendida para uma função analítica em uma vizinhança do ponto zq, definindo g(z0) = 0. A ordem do pólo da função f(z) chama-se a ordem de zero da função jfa. Os teoremas 16 e 18 implicam a seguinte afirmação. Teorema 19. Um fino singular isolado é essencialmente singular se e somente se a parte principal da expansão de Laurent em uma vizinhança pontuada deste ponto contém infinitos termos diferentes de zero. Exemplo 5. O ponto singular da função é zo = 0. Temos Série de Laurent Pontos singulares isolados e sua classificação Portanto, zo = 0 é um ponto singular removível. A expansão da função /(z) em uma série de Laurent na vizinhança do ponto zero contém apenas a parte correta: Exemplo7. f(z) = O ponto singular da função f(z) é zq = 0. Considere o comportamento desta função nos eixos real e imaginário: no eixo real em x 0, no eixo imaginário Portanto, nem finito nem limite infinito f(z) em z -* 0 não existe. Portanto, o ponto r0 = 0 é um ponto essencialmente singular da função f(z). Vamos encontrar a expansão de Laurent da função f(z) em uma vizinhança do ponto zero. Para qualquer C complexo temos We definido. Então a expansão de Laurent contém um número infinito de termos com potências negativas de z.

Modelos descritos por sistemas de duas equações diferenciais autónomas.

plano de fase. Retrato de fase. método da isóclina. principais isóclinas. Estabilidade em estado estacionário. Sistemas lineares. Tipos de ponto-chave: nó, sela, foco, centro. Exemplo: reações químicas de primeira ordem.

Os resultados mais interessantes na modelagem qualitativa das propriedades de sistemas biológicos foram obtidos em modelos de duas equações diferenciais, que permitem um estudo qualitativo usando o método plano de fase. Considere um sistema de duas equações diferenciais ordinárias autônomas da forma geral

(4.1)

P(x,y), Q(x,y)- funções contínuas definidas em algum domínio G plano euclidiano ( x,y- coordenadas cartesianas) e tendo nesta área derivadas contínuas de ordem não inferior à primeira.

Região G pode ser ilimitado ou limitado. Se variáveis x, y têm um significado biológico específico (concentração de substâncias, abundância de espécies), na maioria das vezes a área Gé o quadrante positivo do semiplano direito:

0 £ x< ¥ ,0 £ y< ¥ .

As concentrações de substâncias ou a abundância de espécies também podem ser limitadas de cima pelo volume da embarcação ou pela área do habitat. Então o intervalo de variáveis ​​tem a forma:

0 £ x< x 0 , 0 £ y< y 0 .

Variáveis x, y mudança no tempo de acordo com o sistema de equações (4.1), de modo que cada estado do sistema corresponda a um par de valores de variáveis ​​( x, y).

Por outro lado, para cada par de variáveis ​​( x, y) corresponde a um determinado estado do sistema.

Considere um plano com eixos de coordenadas no qual os valores das variáveis ​​são plotados x,y. cada ponto M este plano corresponde a um determinado estado do sistema. Tal plano é chamado de plano de fase e representa a totalidade de todos os estados do sistema. O ponto M(x, y) é chamado de representação ou ponto de representação.

Deixe no tempo inicial t=t 0 representando as coordenadas do ponto M 0 (x(t 0),y(t 0)). Em cada próximo momento no tempo t o ponto de representação se moverá de acordo com as mudanças nos valores das variáveis x(t),y(t). Conjunto de pontos M(x(t), y(t)) no plano de fase, cuja posição corresponde aos estados do sistema no processo de mudança de variáveis ​​ao longo do tempo x(t), y(t) de acordo com as equações (4.1), é chamado trajetória de fase.

O conjunto de trajetórias de fase para diferentes valores iniciais das variáveis ​​dá um "retrato" facilmente visível do sistema. Prédio retrato de fase permite tirar conclusões sobre a natureza das mudanças nas variáveis x, y sem conhecer as soluções analíticas do sistema original de equações(4.1).

Para representar um retrato de fase, é necessário construir um campo vetorial de direções para as trajetórias do sistema em cada ponto do plano de fase. Especificando um incrementoD t>0,obtemos os incrementos correspondentes D x e D y das expressões:

D x=P(x,y)D t,

D y=Q(x,y)D t.

direção do vetor dy/dx no ponto ( x, y) depende do sinal das funções P(x, y), Q(x, y) e pode ser dada por uma tabela:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Solução desta equação y=y(x,c), ou implicitamente F(x,y)=c, Onde Comé a constante de integração, dá a família de curvas integrais da equação (4.2) - trajetórias de fase sistema (4.1) no plano x, y.

método isoclina

Para construir um retrato de fase, usa-se método isoclina - linhas são desenhadas no plano de fase que cruzam as curvas integrais em um ângulo específico. A equação da isóclina é fácil de obter de (4.2). Vamos colocar

Onde MAS– uma certa constante. Significado MAS representa a tangente da inclinação da tangente à trajetória da fase e pode assumir valores de -¥ para + ¥ . Substituindo em vez de dy/dx em (4.2) a quantidade MAS obtemos a equação isóclina:

.(4.3)

A equação (4.3) determina em cada ponto do plano a única tangente à curva integral correspondente, exceto o ponto onde P(x,y)= 0, Q (x,y) = 0 , em que a direção da tangente se torna indefinida, pois o valor da derivada se torna indefinido:

.

Este ponto é o ponto de intersecção de todas as isoclinas - ponto especial. Simultaneamente anula as derivadas temporais das variáveis x e y.

Assim, no ponto singular, as taxas de variação das variáveis ​​são iguais a zero. Portanto, o ponto singular das equações diferenciais das trajetórias de fase (4.2) corresponde a estado estacionário do sistema(4.1), e suas coordenadas são os valores estacionários das variáveis x, y.

De particular interesse são principais isóclinas:

dy/dx=0, P(x,y)=0 – isoclina de tangentes horizontais e

dy/dx=¥ , Q(x,y)=0 – isoclina de tangentes verticais.

Construindo as principais isoclinas e encontrando o ponto de sua interseção (x,y), cujas coordenadas satisfazem as condições:

encontraremos assim o ponto de interseção de todas as isoclinas do plano de fase, no qual a direção das tangentes às trajetórias de fase é indefinida. Isto - ponto singular, que corresponde estado estacionário do sistema(Fig. 4.2).

O sistema (4.1) tem tantos estados estacionários quantos os pontos de interseção das principais isoclinas no plano de fase.

Cada trajetória de fase corresponde a um conjunto de movimentos de um sistema dinâmico passando pelos mesmos estados e diferindo entre si apenas pelo início da referência de tempo.

Se as condições do teorema de Cauchy forem satisfeitas, então através de cada ponto do espaço x, y, t passa por uma única curva integral. O mesmo é verdade, graças à autonomia, para trajetórias de fase: uma trajetória de fase única passa por cada ponto do plano de fase.

Estabilidade em estado estacionário

Deixe o sistema estar em equilíbrio.

Então o ponto representativo está localizado em um dos pontos singulares do sistema, no qual, por definição:

.

Se um ponto singular é estável ou não é determinado se o ponto representativo sai ou não com um pequeno desvio do estado estacionário. Quando aplicada a um sistema de duas equações, a definição de estabilidade na linguageme, ddo seguinte modo.

O estado de equilíbrio é estável se para qualquer área dada de desvios do estado de equilíbrio (e )área pode ser especificada d (e ), envolvendo o estado de equilíbrio e tendo a propriedade de que nenhuma trajetória que comece dentro da região d , nunca alcançará a fronteira e . (Fig. 4.4)

Para uma grande classe de sistemas - sistemas brutos – cuja natureza do comportamento não muda com uma pequena mudança no tipo de equações, informações sobre o tipo de comportamento nas proximidades do estado estacionário podem ser obtidas estudando não o original, mas o simplificado linearizado sistema.

Sistemas lineares.

Considere um sistema de duas equações lineares:

.(4.4)

Aqui a, b, c, d- constantes, x, y- Coordenadas cartesianas no plano de fase.

A solução geral será procurada na forma:

.(4.5)

Substitua essas expressões em (4.4) e reduza por e eu t:

(4.6)

Sistema algébrico de equações (4.6) com incógnitas A,B tem uma solução diferente de zero somente se seu determinante, composto pelos coeficientes das incógnitas, for igual a zero:

.

Expandindo esse determinante, obtemos a equação característica do sistema:

.(4.7)

A solução desta equação dá os valores do indicadoreu 1,2 , sob o qual valores diferentes de zero são possíveis para UMA e B soluções da equação (4.6). Esses valores são

.(4.8)

Se a expressão do radical for negativa, entãoeu 1,2 números conjugados complexos. Suponha que ambas as raízes da equação (4.7) tenham partes reais diferentes de zero e que não haja raízes múltiplas. Então a solução geral do sistema (4.4) pode ser representada como uma combinação linear de expoentes com expoenteseu 1 , eu 2 :

(4.9)

Para analisar a natureza das possíveis trajetórias do sistema no plano de fase, usamos transformação de coordenadas homogênea linear, o que fará com que o sistema Forma canônica:

,(4.10)

o que permite uma representação mais conveniente no plano de fase em comparação com o sistema original (4.4). Vamos introduzir novas coordenadasξ , η de acordo com as fórmulas:

(4.1)

Sabe-se do curso de álgebra linear que se as partes reais não são iguais a zeroeu 1 , eu 2 o sistema original (4.4) com a ajuda das transformações (4.11) sempre pode ser transformado na forma canônica (4.10) e seu comportamento no plano de fase pode ser estudadoξ , η . Considere os vários casos que podem se apresentar aqui.

Raízes λ 1 , λ 2 – válidos e do mesmo sinal

Neste caso, os coeficientes de transformação são reais, passamos do plano realx,yao plano real ξ, η. Dividindo a segunda das equações (4.10) pela primeira, obtemos:

.(4.12)

Integrando esta equação, encontramos:

Onde .(4.13)

Vamos concordar em entender por λ 2 a raiz da equação característica com um grande módulo, o que não viola a generalidade do nosso raciocínio. Então, como no caso em consideração as raízes λ 1 , λ2 – válidos e do mesmo sinal,uma>1 , e estamos lidando com curvas integrais do tipo parabólica.

Todas as curvas integrais (exceto para o eixo η , que corresponde a ) toque na origem do eixo ξ, que também é uma curva integral da equação (4.11). A origem das coordenadas é um ponto singular.

Vamos agora descobrir a direção do movimento do ponto representativo ao longo das trajetórias de fase. Se λ 1 , λ 2 são negativos, então, como pode ser visto nas equações (4.10), |ξ|, |η| diminuir ao longo do tempo. O ponto representativo aproxima-se da origem, mas nunca a alcança. Caso contrário, isso contradiria o teorema de Cauchy, que afirma que apenas uma trajetória de fase passa por cada ponto do plano de fase.

Um ponto tão singular por onde passam curvas integrais, assim como uma família de parábolas passa pela origem, é chamado de nó (Fig. 4.5)

Estado de equilíbrio do tipo nó em λ 1 , λ 2 < 0 é estável de acordo com Lyapunov, já que o ponto representativo se move ao longo de todas as curvas integrais em direção à origem das coordenadas. isto nó estável. Se λ 1 , λ 2 > 0, então |ξ|, |η| aumenta com o tempo e o ponto representativo se afasta da origem. Neste caso, o ponto singular– nó instável .

No plano de fase x, y o caráter qualitativo geral do comportamento das curvas integrais permanecerá, mas as tangentes às curvas integrais não coincidirão com os eixos coordenados. O ângulo de inclinação dessas tangentes será determinado pela razão dos coeficientes α , β , γ , δ nas equações (4.11).

Raízes λ 1 , λ 2 são válidos e têm sinais diferentes.

Converter de coordenadas x,y para coordenadas ξ, η novamente real. As equações para as variáveis ​​canônicas novamente têm a forma (4.10), mas agora os sinais λ 1 , λ 2 diferente. A equação da trajetória de fase tem a forma:

Onde , (4.14)

Integrando (4.14), encontramos

(4.15)

isto equação define uma família de curvas do tipo hiperbólica, onde ambos os eixos coordenados são as assíntotas (em uma=1 teríamos uma família de hipérboles isósceles). Os eixos coordenados também são curvas integrais neste caso– estas serão as únicas curvas integrais passando pela origem. Cadados quais consiste em três trajetórias de fase: de dois movimentos em direção a um estado de equilíbrio (ou longe de um estado de equilíbrio) e de um estado de equilíbrio. Todas as outras curvas integrais– são hipérboles que não passam pela origem (Fig. 4.6) Este ponto singular é chamado "selim ». As linhas de nível perto da sela da montanha se comportam como trajetórias de fase nas proximidades da sela.

Vamos considerar a natureza do movimento do ponto representativo ao longo das trajetórias de fase próximas ao estado de equilíbrio. Deixe, por exemplo,λ 1 >0 , λ 2<0 . Então o ponto representativo colocado no eixo ξ , se afastará da origem e será colocado no eixo η – se aproximará indefinidamente da origem das coordenadas, sem alcançá-lo em tempo finito. Onde quer que o ponto representativo esteja no momento inicial (com exceção do ponto singular e pontos na assíntota η =0), acabará por se afastar do estado de equilíbrio, mesmo que no início se mova ao longo de uma das curvas integrais em direção a um ponto singular.

é obvio que ponto singular tipo sela é sempre instável . Somente sob condições iniciais especialmente escolhidas na assíntotaη =0 o sistema se aproximará de um estado de equilíbrio. No entanto, isso não contradiz a afirmação de que o sistema é instável. Se você contar, que todos os estados iniciais do sistema no plano de fase são igualmente prováveis, então a probabilidade de tal estado inicial que corresponde ao movimento na direção para ponto singular é igual a zero. Portanto, qualquer movimento real retirará o sistema do estado de equilíbrio.Voltando às coordenadasx,y,obtemos a mesma imagem qualitativa da natureza do movimento das trajetórias em torno da origem.

A fronteira entre os casos considerados de um nó e uma sela é o caso quando um dos indicadores característicos, por exemplo λ 1 , desaparece, o que ocorre quando o determinante do sistema- expressão adbc=0(ver fórmula 4.8 ). Nesse caso, os coeficientes dos lados direitos das equações (4.4) são proporcionais entre si:

e o sistema tem como seus estados de equilíbrio todos os pontos da linha:

As curvas integrais restantes são uma família de linhas paralelas com uma inclinação , ao longo do qual os pontos representativos se aproximam do estado de equilíbrio ou se afastam dele, dependendo do sinal da segunda raiz da equação característica λ 2 = a+d.(Fig.4.7 ) Nesse caso, as coordenadas do estado de equilíbrio dependem do valor inicial das variáveis.

Raízes λ 1 , λ 2 – complexoconjugado

Neste caso, de verdadex e y nós vamos tem conjugados complexos ξ , η (4.10) . No entanto, introduzindo mais uma transformação intermediária, também é possível neste caso reduzir a consideração a uma transformação homogênea linear real. Vamos colocar:

(4.16)

Onde um, b, e você, você – valores reais. Pode-se mostrar que a transformação dex,y para você, você é, sob nossas hipóteses, real, linear, homogêneo com um determinante diferente de zero. por causa das equações(4.10, 4.16) temos:

Onde

(4.17)

Dividindo a segunda das equações pela primeira, Nós temos:

que é mais fácil de integrar, se mudarmos para o sistema de coordenadas polares (r, φ ) . Após a substituição obtemos de onde:

.(4.18)

Assim, no plano de fasevocê, vocêestamos lidando com uma família de espirais logarítmicas, cada uma das quais temponto assintótico na origem.Ponto singular que é o ponto assintótico de todas as curvas integrais com a forma de espirais, amigo aninhado emamigo, liguei foco ( fig.4.8 ) .

Consideremos a natureza do movimento do ponto representativo ao longo das trajetórias de fase. Multiplicando a primeira das equações (4.17) porvocê, e o segundo a v e somando , obtemos:

Onde

Deixar uma 1 < 0 (uma 1 = Réλ ) . O ponto representativo então se aproxima continuamente da origem sem alcançá-la em um tempo finito. Isso significa que as trajetórias de fase são espirais tortuosas e correspondem a oscilações amortecidas variáveis. Isto - foco constante .

No caso de um foco estável, como no caso de um nó estável, não apenas a condição de Lyapunov é satisfeita, mas também um requisito mais rigoroso. Ou seja, para quaisquer desvios iniciais, o sistema eventualmente retornará tão próximo quanto desejado da posição de equilíbrio. Tal estabilidade, na qual os desvios iniciais não só não aumentam, mas decaem, tendendo a zero, é chamada estabilidade absoluta .

Se na fórmula (4.18) uma 1 >0 , então o ponto representativo se afasta da origem, e estamos lidando com foco instável . Ao sair de um aviãovocê, vocêpara o plano de fasex, yespirais também permanecerão espirais, mas serão deformadas.

Considere agora o caso quandouma 1 =0 . Trajetórias de fase no planovocê, vocêhaverá círculos que no aviãox,yajustar elipses:

Assim, emum 1=0 através de um ponto especialx= 0,y= 0 nenhuma curva integral passa. Tal ponto singular isolado, perto do qual as curvas integrais são curvas fechadas, em particular, elipses embutidas umas nas outras e encerrando o ponto singular, é chamado de centro.

Assim, seis tipos de equilíbrio são possíveis, dependendo da natureza das raízes da equação característica (4.7). Visualização das trajetórias de fase no plano x, y para esses seis casos é mostrado na Fig. 4.9.

Arroz. 4.9.Tipos de retratos de fase na vizinhança de um estado estacionário para o sistema de equações lineares (4.4).

Os cinco tipos de estados de equilíbrio são aproximados, sua natureza não muda com mudanças suficientemente pequenas nos lados direitos das equações (4.4). Nesse caso, as mudanças devem ser pequenas não apenas nos membros à direita, mas também em suas derivadas de primeira ordem. O sexto estado de equilíbrio - o centro - não é grosseiro. Com pequenas mudanças nos parâmetros do lado direito das equações, ele passa para um foco estável ou instável.

Diagrama de bifurcação

Vamos introduzir a notação:

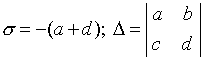. (4.11)

Então a equação característica pode ser escrita na forma:

. (4.12)

Considere um plano com coordenadas cartesianas retangulares s , D e marque nele as áreas correspondentes a um ou outro tipo de estado de equilíbrio, que é determinado pela natureza das raízes da equação característica

.(4.13)

A condição para a estabilidade do estado de equilíbrio será a presença de uma parte real negativa de yeu 1 e eu 2 . Uma condição necessária e suficiente para isso é o cumprimento das desigualdadess > 0, D > 0 . No diagrama (4.15), esta condição corresponde aos pontos localizados no primeiro quarto do plano de parâmetros. O ponto singular será o foco seeu 1 e eu 2 complexo. Esta condição corresponde aos pontos do plano para os quais , Essa. pontos entre dois ramos de uma parábolas 2 = 4 D. Pontos do semi-eixo s = 0, D>0, correspondem a estados de equilíbrio do tipo centro. Da mesma maneira,eu 1 e eu 2 - sinais válidos, mas diferentes, ou seja, um ponto singular será uma sela se D<0, etc. Como resultado, obtemos um diagrama de partição do plano de parâmetros s, D, em regiões correspondentes a diferentes tipos de estados de equilíbrio.

Arroz. 4.10. Diagrama de bifurcação

para o sistema de equações lineares 4.4

Se os coeficientes do sistema linear a, b, c, d depende de algum parâmetro, então quando esse parâmetro for alterado, os valores também mudarãos , D . Ao passar pelos limites, a natureza do retrato de fase muda qualitativamente. Portanto, esses limites são chamados de limites de bifurcação - em lados opostos do limite, o sistema possui dois retratos de fase topologicamente diferentes e, portanto, dois tipos diferentes de comportamento.

O diagrama mostra como essas mudanças podem ocorrer. Se excluirmos casos especiais - a origem das coordenadas - então é fácil ver que a sela pode entrar em um nó estável ou instável ao cruzar o eixo y. Um nó estável pode se mover para uma sela ou um foco estável e assim por diante. Observe que as transições nó estável–foco estável e nó instável–foco instável não são bifurcacionais, pois a topologia do espaço de fase não muda neste caso. Falaremos com mais detalhes sobre a topologia do espaço de fase e transições de bifurcação na Aula 6.

Sob transições de bifurcação, a natureza da estabilidade do ponto singular muda. Por exemplo, um foco estável no centro pode se transformar em um foco instável. Essa bifurcação é chamada Bifurcação de Andronov-Hopf pelos nomes dos cientistas que o estudaram. Com essa bifurcação em sistemas não lineares, nasce um ciclo limite, e o sistema passa a ser auto-oscilante (ver aula 8).

Exemplo. Sistema de reações químicas lineares

Substância x flui de fora a uma taxa constante, transforma-se na substância Y e a uma taxa proporcional à concentração da substância Y, é retirado da esfera de reação. Todas as reações são de primeira ordem, com exceção do influxo de matéria de fora, que tem ordem zero. O esquema de reação se parece com:

(4.14)

e é descrito pelo sistema de equações:

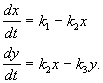(4.15)

Obtemos concentrações estacionárias igualando os lados direitos a zero:

.(4.16)

Considere o retrato de fase do sistema. Dividamos a segunda equação do sistema (4.16) pela primeira. Nós temos:

.(4.17)

A equação (4.17) determina o comportamento das variáveis ​​no plano de fase. Vamos construir um retrato de fase desse sistema. Primeiro, desenhamos as principais isoclinas no plano de fase. Equação da isoclina de tangentes verticais:

Equação para a isoclina de tangentes horizontais:

O ponto singular (estado estacionário) encontra-se na interseção das isoclinas principais.

Agora vamos determinar em que ângulo os eixos coordenados interceptam as curvas integrais.

Se um x= 0, então .

Assim, a tangente da inclinação da tangente às curvas integrais y=y(x), cruzando o eixo y x=0, é negativo no semiplano superior (lembre-se de que as variáveis x, y têm valores de concentração e, portanto, estamos interessados ​​apenas no quadrante superior direito do plano de fase). Neste caso, o valor da tangente do ângulo de inclinação da tangente aumenta com a distância da origem.

Considere o eixo y= 0. Na intersecção deste eixo, as curvas integrais são descritas pela equação

No a tangente da inclinação das curvas integrais que cruzam o eixo das abcissas é positiva e aumenta de zero ao infinito com o aumento x.

No .

Então, com um novo aumento, a tangente da inclinação diminui em valor absoluto, permanecendo negativa e tendendo a -1 em x ® ¥ . Conhecendo a direção das tangentes às curvas integrais nas principais isoclinas e nos eixos coordenados, é fácil construir todo o quadro das trajetórias de fase.

A natureza da estabilidade do ponto singular será estabelecida pelo método de Lyapunov. O determinante característico do sistema tem a forma:

.

Expandindo o determinante, obtemos a equação característica do sistema: , ou seja as raízes da equação característica são ambas negativas. Portanto, o estado estacionário do sistema é um nó estável. Ao mesmo tempo, a concentração da substância x tende a um estado estacionário sempre monotonicamente, a concentração da substância Y pode passar por min ou max. Regimes oscilatórios em tal sistema são impossíveis.

Definição. O ponto singular da função é chamado isolado, se em alguma vizinhança deste ponto existe uma função analítica (ou seja, analítica no anel).

A classificação de pontos singulares isolados de uma função está relacionada ao comportamento desta função na vizinhança de um ponto singular.

Definição. O ponto é chamado descartável um ponto singular de uma função se houver um limite finito dessa função em .

Exemplo 5 Mostre que a função tem uma singularidade removível em um ponto.

Solução. Recordando o primeiro limite notável, calculamos

Isso significa que a função dada tem uma singularidade removível no ponto.

Tarefa 4. Mostre que o ponto é removível para .

Definição. O ponto é chamado pólo função , se esta função aumenta indefinidamente para , ou seja .

Atentemos para a conexão entre os conceitos de zero e pólo de uma função analítica. Vamos representar a função como .

Se um ponto é um zero simples de uma função, então a função tem um pólo simples

Se o ponto é de ordem zero para a função, então para a função é o pólo ordem.

Exemplo 6 Mostre que a função tem um pólo de terceira ordem em um ponto.

Solução. Supondo , obtemos . Como tendemos a zero, de acordo com qualquer lei, temos . Então , e com ela a própria função aumenta indefinidamente. Portanto, , ou seja, o ponto singular é um pólo. Para uma função, este ponto é obviamente um zero triplo. Portanto, para esta função, o ponto é um pólo de terceira ordem.

Tarefa 5. Mostre que o ponto tem um pólo simples.

Definição. O ponto é chamado essencialmente especial ponto da função se neste ponto não existe limite finito nem infinito da função (o comportamento da função não está definido).

Let Ser um ponto singular essencial da função . Então, para qualquer número complexo pré-atribuído, existe uma sequência de pontos que convergem para , ao longo da qual os valores tendem a : ( teorema de Sochocki).

Exemplo 7 Mostre que uma função em um ponto tem uma singularidade essencial.

Solução. Considere o comportamento de uma dada função na vizinhança do ponto. Pois ao longo da parte positiva do eixo real (ou seja, ) temos e ; se ao longo da parte negativa do eixo real (isto é), então e . Portanto, não há limite para . Por definição, uma função tem uma singularidade essencial em um ponto.

Consideremos o comportamento da função no zero do ponto de vista do teorema de Sochocki. Let Ser qualquer número complexo diferente de zero e infinito.

Da igualdade encontramos . Assumindo , obtemos uma sequência de pontos , . Obviamente, . Em cada ponto dessa sequência, a função é igual a , e portanto

Tarefa 6. Mostre que a função tem uma singularidade essencial em um ponto.

Um ponto no infinito é sempre considerado especial para a função. Um ponto é chamado de ponto singular isolado de uma função se esta função não possui outros pontos singulares fora de algum círculo centrado na origem.

A classificação de pontos singulares isolados também pode ser estendida ao caso.

Exemplo 8 Mostre que a função tem um pólo duplo no infinito.

Solução. Considere a função , onde é uma função analítica em uma vizinhança do ponto , e . Isso significa que a função tem um zero duplo no infinito, mas para a função o ponto é um pólo duplo.

Exemplo 9 Mostre que a função tem uma singularidade essencial no infinito.

Solução. Um problema semelhante é considerado na pr.7. Considere o comportamento de uma função na vizinhança de um ponto infinitamente distante. Para ao longo da parte positiva do eixo real e para ao longo da parte negativa do eixo real. Isso significa que não há limite da função em um ponto e, em virtude da definição, esse ponto é essencialmente singular.

A natureza da singularidade de uma função em um ponto pode ser julgada por parte principal Expansão Laurent em um bairro deste ponto.

Teorema 1. Para que o ponto seja descartável ponto singular da função , é necessário e suficiente que a correspondente expansão de Laurent não continha a parte principal.

Tarefa 6. Usando a expansão de Taylor da função em uma vizinhança do ponto , mostre que ela tem uma singularidade removível em zero.

Teorema 2. Para que o ponto seja pólo funções, é necessário e suficiente para que parte principal expansão Laurent correspondente continha um número finito de membros :

O número do maior termo negativo determina a ordem do polo.

Neste caso, a função pode ser representada como

onde é a função analítica no ponto, , é a ordem do pólo.

Exemplo 10 Mostre que a função tem pólos simples nos pontos.

Solução. Vamos considerar um ponto. Usamos a expansão de Laurent desta função nas proximidades deste ponto, obtida no Exemplo 2:

Como a maior (e única) potência negativa na parte principal dessa expansão é igual a um, o ponto é um simples pólo dessa função.

Este resultado poderia ter sido obtido de outra forma. Vamos representar na forma e colocar - esta é uma função que é analítica no ponto e . Portanto, devido a (8) esta função tem um pólo simples no ponto.

Outra maneira: considere uma função que tenha um zero simples no ponto. Portanto, neste ponto, ele tem um pólo simples.

Da mesma forma, se escrevermos a função na forma , onde é uma função analítica no ponto e , fica imediatamente claro que o ponto é um pólo simples da função .

Tarefa 7. Mostre que a função tem um pólo de 2ª ordem no ponto e um pólo de 4ª ordem no ponto .

Teorema 3. Para que o ponto seja essencialmente especial ponto da função , é necessário e suficiente que parte principal Expansão de Laurent em uma vizinhança do ponto continha um número infinito de membros .

Exemplo 11. Determine a natureza da singularidade no ponto da função

Solução. Na conhecida expansão do cosseno, colocamos no lugar de:

Portanto, a expansão de Laurent na vizinhança de um ponto tem a forma

Aqui a parte correta é um termo. E a parte principal contém um número infinito de termos, então o ponto é essencialmente singular.

Tarefa 8. Mostre que em um ponto a função tem uma singularidade essencial.

Considere alguma função e anote sua expansão de Laurent no ponto:

Vamos fazer uma substituição, enquanto o ponto vai ao ponto. Agora, na vizinhança de um ponto no infinito, temos

Resta introduzir uma nova designação. Nós temos

onde é a parte principal e é a parte regular da expansão de Laurent da função na vizinhança de um ponto infinitamente distante. Assim, na expansão de Laurent de uma função na vizinhança de um ponto, a parte principal é uma série em potências positivas, enquanto a parte correta é uma série em potências negativas. Levando isso em conta

No entanto, os critérios acima para determinar a natureza da singularidade permanecem válidos para um ponto infinitamente distante.

Exemplo 12. Descubra a natureza da singularidade da função no ponto. , então, em um ponto, pode se tornar não isolado.

Exemplo 15 A função em um ponto infinitamente distante tem uma singularidade essencial. Mostre que o ponto para a função não é um ponto singular isolado.

Solução. A função tem um número infinito de pólos nos zeros do denominador, ou seja, nos pontos , . Desde , então o ponto , em qualquer vizinhança da qual existem pólos , é o ponto limite para os pólos.

ponto singular

Na matemática.

1) Ponto singular da curva dada pela equação F ( x, y) = 0, - ponto M 0 ( x 0 , y 0), em que ambas as derivadas parciais da função F ( x, y) desaparecer:

Se, além disso, nem todas as segundas derivadas parciais da função F ( x, y) no ponto M 0 são iguais a zero, então O. t. é chamado de duplo. Se, juntamente com o desaparecimento das primeiras derivadas no ponto M 0, todas as segundas derivadas desaparecem, mas nem todas as terceiras derivadas são iguais a zero, então o O. t. é chamado triplo e assim por diante. Ao estudar a estrutura de uma curva perto de um duplo O. t., um papel importante é desempenhado pelo sinal da expressão

Se Δ > 0, então o O. t. é chamado de isolado; por exemplo, a curva y 2 - x 4 + 4x 2= 0 a origem é um O. t. isolado (ver arroz. 1 ). Se Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 a origem das coordenadas é o nodal O. t. (ver arroz. 2 ). Se Δ = 0, então a curva O. t. é isolada ou caracterizada pelo fato de que diferentes ramos da curva têm uma tangente comum neste ponto, por exemplo: tangente e formam um ponto, como uma curva y 2 - x 3= 0 (ver arroz. 3 , uma); b) cúspide do 2º tipo - diferentes ramos da curva estão localizados no mesmo lado da tangente comum, como uma curva (y - x 2)2 - x 5= 0 (ver arroz. 3 , b); c) ponto de auto-contato (para uma curva y 2 - x 4= 0 origem é um ponto de autocontato; (cm. arroz. 3 , dentro). Junto com o O. t. especificado, existem muitos outros O. t. com nomes especiais; por exemplo, um ponto assintótico é o vértice de uma espiral com um número infinito de voltas (ver Fig. arroz. quatro ), ponto de quebra, ponto de canto, etc.

2) Um ponto singular de uma equação diferencial é um ponto no qual tanto o numerador quanto o denominador do lado direito da equação diferencial desaparecem simultaneamente (Veja Equações Diferenciais)

onde P e Q são funções continuamente diferenciáveis. Assumindo O. t. localizado na origem das coordenadas e usando a fórmula de Taylor (Ver fórmula de Taylor), podemos representar a equação (1) na forma

onde P 1 ( x, y) e Q 1 ( x, y) são infinitesimais em relação a

Ou seja, se λ 1 ≠ λ 2 e λ 1 λ 2 > 0 ou λ 1 = λ 2, então O. t. é um nó; todas as curvas integrais que passam por pontos de uma vizinhança suficientemente pequena do nó entram nele. Se λ 1 ≠ λ 2 e λ 1 λ 2 i β, α ≠ 0 e β ≠ 0, então O. t. é um foco; todas as curvas integrais que passam por pontos em uma vizinhança suficientemente pequena do foco são espirais com um número infinito de voltas em qualquer vizinhança arbitrariamente pequena do foco. Se, finalmente, λ 1,2 = ± euβ, β ≠ 0, então o caráter de O. t. não é determinado por termos lineares em expansões de P ( x, y) e Q ( x, y), como aconteceu em todos os casos anteriores; aqui O. t. pode ser um foco ou centro, ou pode ter um caráter mais complexo. Na vizinhança do centro, todas as curvas integrais são fechadas e contêm o centro dentro delas. Então, por exemplo, o ponto (0, 0) é um nó para as equações no" = 2u/x(λ 1 = 1, λ 2 = 2; ver arroz. 5 , a) e y" = u/x(λ 1 = λ 2 = 1; ver arroz. 5 , b), uma sela para a equação y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. arroz. 6 ), o foco para a equação y" =(x + y) / (x - y) (λ 1 = 1 - eu, λ 2 = 1 + eu; cm. arroz. 7 ) e o centro da equação y" = -x / y(λ 1 = -eu, λ 2 = eu; cm. arroz. oito ).

Se x, y) e Q ( x, y) são analíticos, a vizinhança de um O. t. de ordem superior pode ser dividida em regiões: D 1 - preenchido com curvas integrais, ambas as extremidades entrando no O. t. (regiões elípticas), D 2 - preenchido com curvas integrais, uma extremidade entrando no O. t. (regiões parabólicas) e D 3 - regiões delimitadas por duas curvas integrais incluídas no O. t., entre as quais existem curvas integrais do tipo de hipérboles (regiões hiperbólicas) (ver. arroz. 9 ). Se não houver curvas integrais entrando em um ponto O., então o ponto O. é chamado de ponto de tipo estável. A vizinhança de um O. t. estável consiste em curvas integrais fechadas contendo O. t. dentro de si, entre as quais espirais estão localizadas (ver Fig. arroz. dez ).

O estudo das equações diferenciais de O. t., ou seja, em essência, o estudo do comportamento de famílias de curvas integrais em uma vizinhança de O. t. M. Lyapunov a, A. Poincaré e outros).

3) Um ponto singular de uma função analítica de valor único é um ponto no qual a analiticidade da função é violada (ver funções analíticas). Se houver um bairro de O. t. uma, livre de outro O. t., então o ponto umaé chamado O. t. isolado. Se umaé um O.T. isolado e existe um O.T. finito é chamado de O.T removível. Ao alterar apropriadamente a definição da função no ponto a (ou redefinindo-a neste ponto, se a função não estiver definida nele), ou seja, definindo f(uma)= b, é possível atingir uma se tornará um ponto ordinário da função corrigida. Por exemplo, ponto z= 0 é um O.T. removível para a função f 1 ( z) = f(z), E se z≠ 0, e f 1(0),=1, ponto z= 0 é um ponto ordinário [ f 1 (z) é analítico no ponto z= 0]. Se um uma- O. t. isolado e a é chamado de pólo ou um ponto essencialmente singular da função f(z), se a série de Laurent) funciona f(z) em uma vizinhança de um O. t. isolado não contém potências negativas z - um, E se uma- removível O. t., contém um número finito de potências negativas z - um, E se uma- pólo (neste caso, a ordem do pólo Ré definido como a maior potência de a - um ponto essencialmente singular. Por exemplo, para a função

p = 2, 3, …)

ponto z= 0 é o pólo da ordem R, para a função

ponto z= 0 é um ponto singular essencial.

Na fronteira do círculo de convergência de uma série de potências deve haver pelo menos um O. t. da função representada dentro deste círculo pela série de potências dada. Todos os pontos de fronteira do domínio de existência de uma função analítica de valor único (fronteira natural) são pontos de fronteira desta função. Assim, todos os pontos do círculo unitário | z| = 1 são especiais para a função

Para uma função analítica multivalorada, o conceito de "O. t." mais difícil. Além do O. t., em folhas individuais da superfície de Riemann de uma função (ou seja, o O. t. de elementos analíticos de valor único), qualquer ponto de ramificação também é um O. t. da função. Pontos de ramificação isolados de uma superfície de Riemann (isto é, pontos de ramificação tais que em algumas de suas vizinhanças não existem outras funções O.t. em qualquer folha) são classificados como segue. Se a é um ponto de ramificação isolado de ordem finita e existe um a finito, ele é chamado de pólo crítico. Se um umaé um ponto de ramificação isolado de ordem infinita, e a é chamado de transcendental O. t. Todos os outros pontos de ramificação isolados são chamados de pontos críticos essencialmente singulares. Exemplos: ponto z= 0 é um ponto crítico ordinário da função f ( z) = registro z e um ponto crítico singular essencial da função f (z) = log do pecado z.

Qualquer O. t., exceto um removível, é um obstáculo para a continuação analítica, ou seja, a continuação analítica ao longo de uma curva que passa por um O. t. irremovível é impossível.

Grande Enciclopédia Soviética. - M.: Enciclopédia Soviética. 1969-1978 .

Veja o que é "Ponto Especial" em outros dicionários:

Pontos aqui. Veja também ponto singular (equações diferenciais). Uma característica ou singularidade em matemática é um ponto no qual um objeto matemático (geralmente uma função) não é definido ou tem comportamento irregular (por exemplo, um ponto no qual ... ... Wikipedia

Uma função analítica é um ponto no qual as condições de analiticidade são violadas. Se uma função analítica f(z) é definida em alguma vizinhança do ponto z0 em qualquer lugar … Enciclopédia Física

Uma função analítica é o ponto em que a analiticidade de uma função é violada... Grande Dicionário Enciclopédico

ponto singular- — [Ya.N. Luginsky, M.S. Fezi Zhilinskaya, Yu.S. Kabirov. Dicionário Inglês-Russo de Engenharia Elétrica e Indústria de Energia, Moscou, 1999] Tópicos de engenharia elétrica, conceitos básicos EN ponto singular ... Manual do Tradutor Técnico

1) Um OT de uma função analítica f(z) é um obstáculo à continuação analítica de um elemento da função f(z) de uma variável complexa z ao longo de algum caminho no plano dessa variável. Seja a função analítica f(z) definida por algum ... ... enciclopédia matemática

Uma função analítica, o ponto em que a analiticidade da função é violada. * * * PONTO SINGULAR Um PONTO SINGULAR de uma função analítica, um ponto no qual a analiticidade da função é violada ... dicionário enciclopédico

ponto singular- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. ponto singular vok. singularer Punkt, m rus. ponto singular, fpranc. partícula pontual, m; point singulier, m … Automatikos terminų žodynas

Deixar zq - ponto singular da função f(z), t.s. f(z) mas é analítico neste ponto (em particular, pode não ser definido nele). Se existe tal vizinhança perfurada do ponto zq (ou seja, o conjunto O z - zq f(z) é aliatico, então zo chamado ponto singular isolado funções f(z). Esta definição também é preservada no caso zn = oo, se o iodo é uma vizinhança perfurada de um ponto zq = oo entender o conjunto z > EU - a aparência de algum círculo centrado na origem. Em outras palavras, o ponto singular zq é dito isolado se existe uma vizinhança deste ponto na qual existem outros pontos singulares diferentes de zq. Em todos os lugares abaixo, consideramos apenas pontos singulares de um caractere de valor único (a função f(z) considerado único).

Dependendo do comportamento da função f(z) no z -> zq Existem três tipos de pontos singulares. Ponto singular isolado funções zq f(z) chamado:

1) ponto singular removível se existe um limite finito

2) pólo se houver um limite

3) ponto essencial, E se f(z) não tem limite finito nem infinito para z-> zq.

EXEMPLO 26.1. Vamos mostrar que todos os três tipos de pontos singulares são realizados. Considerar f(z)= ponto zq = 0 é isolado

ponto singular desta função. Usando a fórmula (22.12), obtemos a expansão

de onde se conclui que existe lim fi(z)= 1. Portanto, zq = 0 é

é um ponto singular removível da função fi(z).

Função f'j(z) =--- tem um pólo em um ponto zo= 1 porque

2 r“ X

Considere agora a função )z(z)= e 1 ^ r e mostre que zo = O é um ponto singular essencial desta função. Ao se esforçar z a zero ao longo do eixo real, os limites esquerdo e direito da função f (z) diferente: lim Com 1 / 1 = 0,lim com 1 /* = os. Isso implica,

x->0-0 x->0+0

o que f:i(z) não tem limite finito nem infinito para 2 -> Ah, ou seja zq = 0 é um ponto essencialmente singular desta função. (Observe que conforme o ponto tende z-iy a zero na função do eixo imaginário

não tem limite algum.)

Claro, também existem pontos singulares não isolados. Por exemplo. função tem pólos em pontos z n = -, P= ±1, ±2,...

Consequentemente, Zq = 0 é um ponto singular não isolado desta função: em qualquer vizinhança (arbitrariamente pequena) deste ponto existem outros pontos singulares g pág.

Deixar zo- ponto singular isolado final de uma função f(z). Então f(z)é semelhante em alguma vizinhança perfurada 0 Zo do ponto zo esta vizinhança pode ser considerada como um anel com raio interno r = 0. Pelo Teorema 25.1, na vizinhança considerada, a função f(z) pode ser expandido em uma série de Laurent (25.2). Mostraremos que o comportamento da função para 2 -> zq (ou seja, o tipo de ponto singular zo) depende da forma da parte principal da decomposição (25.2); esta circunstância explica a origem do termo “parte principal”.

TEOREMA 2G.2. Um ponto singular isolado zo de uma função f(z) é removível se e somente se a expansão Lorap em uma vizinhança perfurada deste ponto tem o oid

Essa. consiste apenas na parte correta, e todos os coeficientes da parte principal são iguais à bala.

Prova. 1. Deixe zoé um ponto singular removível. Provemos que a expansão de Laurent da função f(z) tem a forma (26.1). Desde o ponto singular zo removível, então existe um limite finito lim f(z) = A. Consequentemente, f(z) limitado em alguma vizinhança pontuada 0 z - zq do ponto zo, Essa. )(z) para todos z deste bairro. Pegue qualquer R. U р /?|, e use as fórmulas (25.3) para os coeficientes da série de Laurent:

Para os coeficientes da parte principal da expansão n =- 1,-2,... Para tais valores P temos p~n-e 0 em R-> 0. Como o valor R pode ser escolhido arbitrariamente pequeno, então Senhor ~" pode ser arbitrariamente pequeno. Como |c t,| ^ Sr~n e cn não dependem de p, então cn = 0 para e= - 1, -2,..., que estava para ser provado.

2. Suponhamos agora que a expansão de Laurent tem a forma (26.1). A série (26.1) é uma série de potências e. portanto, converge não só nos puncionados, mas também em toda a vizinhança z-zq incluindo o ponto zo; sua soma S(z)é analítico para z e S(z) = )(z) em 0 z - zo R. Portanto, existe um limite finito lim )(z)\u003d Pm 5 (r) \u003d 5 (r) - Portanto, o ponto singular zq

Z->Zo Z-*Zo

descartável. O teorema foi provado.

Comente. Segue-se da prova do teorema que em uma vizinhança perfurada 0 z - zo de um ponto singular removível, a função f(z) coincide com a função S(r), que é analítica em toda a vizinhança z - zo . Portanto, se colocarmos /(th) = S(zq), então, sem alterar os valores da função f(z) em qualquer ponto da vizinhança puncionada, tornamos esta função analítica em r, ou seja, "remover" o recurso. Isso explica o termo “singularidade removível”. É natural considerar tais pontos como regulares, e não como pontos singulares da função f(z).

Considere, por exemplo, a função

No exemplo 26.1, foi mostrado que Pm (n) = 1. i.e. ponto singular

zq = 0 é removível. Definindo /i(0) = 1, eliminamos a singularidade e obtemos uma função que é analítica no ponto zq = 0 (e em todo o plano C).

Vamos agora caracterizar os polos em termos de expansões de Laurent.

Teorema 26.3. Um ponto singular isolado Zo de uma função f(z) é um pólo se e somente se, quando a parte principal da expansão de Laurent com centro Zq tem apenas um número finito de distintos

de coeficientes zero com n:

Prova. 1. Deixe zq - pólo, ou seja lim /( z) = oo.

Provemos que a expansão de Laurent da função f(z) tem a forma (2G.2). desde lim f(z)= oi. então existe uma vizinhança perfurada do ponto

ki zq. em que f(z)é analítico e não tem zeros. Então a função g(z) = 1 /f(z) também será analítico neste bairro perfurado, e lim g(z)= 0. Portanto, Zoé descartável *-? *0

ponto singular da função g(z). vamos redefinir g(z) no ponto zo, colocando g(zo)= 0. Então g(z) torna-se analítico em toda a vizinhança do ponto (não perfurado) z 0 , e z0 será o seu zero isolado. denotar por N multiplicidade (ordem) desse zero. Como foi mostrado em §23, em uma vizinhança do ponto função zq g(z) representável na forma (ver (23.2))

e (z$) f 0 e y>(z)é analítico em alguma vizinhança do ponto zo- Porque ip(z) contínuo no ponto zo e g>(zo) F 0" então ip(z) também não tem zeros em alguma vizinhança deste ponto. Portanto função 1 /-p(z) também será analítico nesta vizinhança e, portanto, se expande nela em uma série de Taylor:

Abrindo os colchetes e alterando as designações dos coeficientes, escrevemos a última expansão na forma

onde c_jv = 1>o f 0. Assim, a parte principal da expansão de Laurent de f(r) contém apenas um número finito de termos; chegamos à igualdade exigida (26.2).

2. Deixe entrar uma vizinhança perfurada de um ponto º função )(z)é representado pela expansão de Laurent (26.2) (em uma forma mais expandida, veja (26.3)), cuja parte principal contém apenas um número finito de termos, e Com- d" f 0. Devemos provar que Zq - pólo de função f(z). Multiplicando a igualdade (26.3) por (G - G o) iV , obtemos a função

A série em (26.4) é uma série de potências convergindo para uma função analítica não apenas no puncionado, mas também em toda a vizinhança do ponto Zq. Portanto, a função h(z) torna-se analítico neste bairro se o estendermos em th definindo h(zo)= s_dg f 0. Então

Assim, o ponto o é um pólo, e o Teorema 26.3 está provado.

Multiplicidade (ordem) da função zero g(z)= 1//(r) é chamado ordem dos pólos função /(r). Se um N- a ordem do pólo é th, então g(z)= (r- Zo)Nip(z), e ir) F 0, e, como mostrado na primeira parte da prova do Teorema 26.3, a expansão de f(r) tem a forma (26.3), onde c_/v f 0. Inversamente, se f(r) se expande na série (26.3) e e-z F 0, então

s.t. N- a ordem do pólo da função f(r). Nesse caminho, a ordem do pólo zq da função/(G) é igual ao número do coeficiente líder diferente de zero da parte principal da expansão de Laurent na vizinhança pontuada do ponto zq(ou seja, igual a tal número N, o que s_dg f 0 e sp= 0 em P > n).

Vamos provar a seguinte afirmação, que é conveniente) para aplicações.

Corolário 26.4. O ponto zq é um pólo de ordem N da ficção/(G) se e apenas se/(G) representar na forma

onde h(z) é uma função analítica em uma vizinhança de um pontoº e h(zo) f 0.

Prova. Função cp(z) = l/h(z)é analítico em alguma vizinhança do ponto r. A condição do Corolário 26.4 é equivalente ao seguinte:

É por isso zq - multiplicidade zero N funções g(z). e, portanto, o pólo de multiplicidade N funções /(2).

II exemplo 26.5. Encontrar pontos singulares isolados de uma função e determinar o seu tipo.

D e u ção. Os pontos em que (z 2 + 1 )(z+ H) 2 = 0. Se z 2 EU- 1 = 0 então 2 = ±r E se (z 4- H) 2 = 0, então z= -3. Portanto, a função tem três pontos singulares z= r, 22 = -r, Z3 = - 3. Considere z:

G- pólo de primeira ordem (usamos o Corolário 26.4). Pode-se provar similarmente que 22 = -eu também um pólo de primeira ordem. Para 2h temos:

Passemos à consideração de pontos essencialmente singulares.

Teorema 26.6. Um ponto singular isolado zq de uma função f(z) é essencialmente singular se e somente se a parte principal da expansão de Laurent centrada em zq tem infinitamente muitos diferentes de. zero, coeficientes com p.

Prova. O teorema 26.6 segue diretamente dos teoremas 26.2 e 26.3. Com efeito, se o ponto zq é essencialmente singular, então a parte principal da expansão de Laurent não pode estar ausente ou conter um número finito de termos (caso contrário, o ponto Zq será removível ou poste). Portanto, o número de termos na parte principal deve ser infinito.

Por outro lado, se a parte principal contém infinitos membros, então Zq não pode ser um ponto removível nem um pólo. Consequentemente, este ponto é essencialmente singular.

De acordo com a definição, um ponto essencialmente singular é caracterizado pelo fato de que a função f(2) não tem limite finito nem infinito para z ->zq. Uma ideia mais completa de quão irregular é o comportamento de uma função em uma vizinhança de um ponto essencialmente singular é dada pelo seguinte teorema.

Teorema 26.7 (teorema de Sochocki). Se zq é essencialmente singular, então o ponto da função f(z), então para qualquer número complexo EU, incluindo A = oo, existe uma sequência de pontos z n tal que z n -> zo e lim f(zn) = MAS.

n->os

Prova. Considere primeiro o caso A = oo. Na primeira parte da prova do Teorema 2G.2, estabelecemos que se f(z)é limitado em alguma vizinhança perfurada do ponto r0, então todos os coeficientes c, n = - 1, - 2,... da parte principal são iguais a zero (e, conseqüentemente, a singularidade em th é removível). Visto que por suposição r0 é um ponto essencialmente singular, a função f(r) é ilimitada em qualquer vizinhança pontuada do ponto r0. Tomemos uma vizinhança estreita 0 Z tal que f(zi) > 1 (se |/(r)| z - zo R/2 existe um ponto z-2 , onde |/(dd)| > 2, etc.: no bairro perfurado O 71. É óbvio que rn -e go e lim /(r«) = oo. Assim, no caso A = oo, Teorema 26.7

comprovado.

Deixe agora A f oo. Assuma primeiro que existe uma vizinhança perfurada 0

= -aaa---- será analítico nesta vizinhança perfurada e, consequentemente,

/(G) - MAS

conseqüentemente, r é um ponto singular isolado da função Φ(r). Vamos mostrar. que r0 é um ponto essencialmente singular de Φ(r). Deixe estar errado. Então existe um limite lim Φ(r), finito ou infinito. Porque

/(r) = A + , então Hsh /(r) também existe, o que contradiz a condição

F(g) ~ :-*z 0

vista do teorema. Assim, r0 é um ponto essencialmente singular da função Φ(r). Conforme provado acima, existe uma sequência de pontos r n tal que r n o e lim Φ(r n) = oo. Daqui

Provamos a afirmação exigida sob a suposição de que f(r) F A em alguma vizinhança perfurada do ponto r. Vamos agora assumir que isso não é verdade, ou seja, em qualquer vizinhança perfurada arbitrariamente pequena do ponto em que existe tal ponto G", que f(r") = A. Então, para qualquer P na vizinhança perfurada 0 f(z u) = L. Assim, a afirmação exigida é verdadeira P-yuo

em todos os casos, e o Teorema 26.7 está provado.

De acordo com o Teorema 26.7 (de Sokhotsky), em qualquer vizinhança perfurada (arbitrariamente pequena) de um ponto essencialmente singular, a função f(r) assume valores arbitrariamente próximos de qualquer número no plano complexo estendido C.

Para estudar pontos singulares isolados, as conhecidas expansões de Taylor de funções elementares básicas são frequentemente úteis.

EXEMPLO 2G.8. Determine o tipo de ponto singular zq = 0 para a função

Resolvido e e. Expandimos o numerador e o denominador em uma série de Taylor em potências de r. Substituindo em (22.11) 3 z em vez de r e subtraindo 1, obtemos

Usando (22.12), obtemos a expansão do denominador:

As séries nessas expansões convergem em todo o plano complexo €. Nós temos

e /2(2) são análogos em uma vizinhança do ponto zo = 0 (e mesmo em todo o plano) e /2(20) F 0, então h(z) também é analítico em alguma vizinhança do ponto gF 0. De acordo com o Corolário 26.4, o ponto Zo = 0 é o pólo da ordem N = 4.

II exemplo 26.9. Encontrar pontos singulares de uma função f(z)= sin j - e determine seu tipo.

P e em e e e. A função tem um único ponto singular final zq = 1. Em outros pontos de C, a função w =--- analítico; daí a função pecado W será analítico.

Substituindo na expansão do seno (22.12) - ao invés de r, obtemos

Obtivemos a expansão da função sen em uma série de Laurent em uma vizinhança pontuada do ponto 20 = 1. Como a expansão resultante contém infinitos termos com potências negativas (r - 1), então zq = 1 é um ponto singular essencial (neste caso, a expansão de Laurent consiste apenas na parte principal e a parte correta está ausente).

Observe que neste caso também foi possível estabelecer a natureza da singularidade diretamente da definição, sem recorrer à expansão em série. De fato, existem sequências (r") e (2") convergindo para zo= 1, e tal que f(z"n)= 1, /(2") = 0 (especifique essas sequências você mesmo). Então, f(z) não tem limite quando z -> 1 e, portanto, o ponto zq - 1 é essencialmente singular.

Vamos introduzir o conceito de expansão de Laurent de uma função na vizinhança de um ponto Zq = 00 e considere a conexão entre a expansão e a natureza da singularidade neste ponto. Observe que as definições de um ponto singular isolado e seu tipo (removível, polo ou essencialmente singular) são transportadas para o caso zq = oc inalterado. Mas o Teorema 26.2. 26.3 e 26.6, relacionados à natureza das expansões de Laurent, precisam ser alterados. A questão é que os membros c n (z - 2o) pág. P= -1,-2,..., a parte principal, definindo a "'irregularidade" da função próximo ao ponto final Zq, como 2 tende a oo, eles se comportarão “corretamente” (tendem a 0). Pelo contrário, os membros do regular partem com P= 1,2,... tenderá a oo; eles determinam a natureza da singularidade em Zq = oo. Portanto, a maior parte da expansão na vizinhança de oo serão os termos com potências positivas P, e correto - com negativo.

Vamos introduzir uma nova variável w = 12. Função tv= 1/2, estendido de modo que u(oo) = 0, um-para-um e mapeia conformemente a vizinhança z > R pontos zq = 00 na vizinhança de |w| wq = 0. Se a função f(z) análise em um bairro perfurado R z Zq = oc, então a função G(w) = f(l/w) será analítico na vizinhança amarela 0 wo = 0. Já que para 2 -> oo haverá W-> 0, então

É por isso G(w) tem no ponto wq = 0 é uma singularidade do mesmo tipo que f(z) no ponto Zq = 00. Vamos expandir a função G(w) em uma série de Laurent em uma vizinhança pontuada do ponto wo = 0:

As somas do lado direito de (26.5) representam as partes correta e principal da expansão, respectivamente. Vamos para a variável z, substituindo w = 1/z:

denotando P\u003d -A *, 6 * \u003d 6_ " \u003d com p e percebendo que G(l/z) = f(z), Nós temos

A decomposição (2G.G) é chamada Expansão de Laurent da função f(z) em uma vizinhança perfurada do ponto zq= oi. A primeira soma em (2G.6) é chamada parte direita, e a segunda soma é parte principal essa decomposição. Como essas somas correspondem às partes corretas e principais da expansão (26.5), a expansão (26.6) satisfaz os análogos dos Teoremas 26.2, 26.3 e 26.6. Assim, o seguinte teorema é um análogo do Teorema 26.2.

Teorema 26.10. Ponto singular isoladoZq - os (funções/(G) é removível se e somente se a expansão de Laurent em uma vizinhança perfurada deste ponto tem a forma

s.t. consiste apenas na parte correta.

Colocamos /(oo) = co. A função definida pela série (26.7) convergindo na vizinhança z > R pontos 2o \u003d oc, chamados analítico no ponto z o = oo. (Observe que esta definição é equivalente à analiticidade da função G(w) no ponto ai = 0.)

Exemplo 26.11. Investigue o ponto singular zq = oo da função

Como o limite é finito, então zo = oo é um ponto singular removível da função f(r). Se colocarmos /(oo) = lim J(z)= 0, então f(z) se tornará

tique no ponto Zo= os. Vamos mostrar como encontrar a expansão correspondente (26.7). Vamos para a variável W = 1 fz. Substituindo z= 1 /?e, obtemos

(a última igualdade é válida na vizinhança puncionada do ponto ww = 0, mas vamos estender a definição (7(0) = 0). A função resultante tem pontos singulares w =±i, w =-1/3, e no ponto Wq = 0 é analítico. Função de expansão G(w) por graus W(como foi feito no Exemplo 25.7) e substituindo na série de potência resultante w = 1/z pode-se obter a expansão (26.7) da função f(z).

Teorema 26.3 para o caso zo= oo será reescrito da seguinte forma.

Teorema 26.12. Ponto singular isolado ir = os a função f(z) é um pólo se e somente se a parte principal da expansão de Laurent (26.6) tem apenas um número finito de coeficientes diferentes de zero Com":

Aqui a série é a parte regular e o polinômio entre parênteses é a parte principal da expansão. A multiplicidade do pólo em oc é definida como a multiplicidade do pólo wq = 0 funções G(z).É fácil ver que a multiplicidade do pólo coincide com o número N em (26.8).

Q p | (i 2 + 1) (z + 3) 2

Uma tarefa. Mostre que a função f(z) =-- -- Tem em

ponto zo = oo ordem dos pólos 3.

O teorema 26.6 sobre um ponto singular essencial é reescrito para o caso zo= os quase literalmente, e não nos debruçamos sobre isso em detalhes.